题目内容
4.在等差数列{an},an=11-2n,求数列{|an|}的前n项和Tn.分析 当n≤5时,|an|=an=11-2n,当n>5时,an=11-2n<0;从而分类讨论求前n项和.
解答 解:当n≤5时,an=11-2n>0,
则|an|=an=11-2n,
则Tn=$\frac{9+11-2n}{2}$n=(10-n)n;
当n>5时,an=11-2n<0,
则|an|=an=2n-11,
则Tn=|a1|+|a2|+|a3|+|a4|+|a5|+|a6|+|a7|+…+|an|
=a1+a2+a3+a4+a5-a6-a7-…-an;
=2(a1+a2+a3+a4+a5)-(a1+a2+a3+a4+a5+a6+a7+…+an)
=50-(10-n)n
=n2-10n+50.
故Tn=$\left\{\begin{array}{l}{(10-n)n,n≤5}\\{{n}^{2}-10n+50,n>5}\end{array}\right.$.
点评 本题考查了绝对值数列的化简运算的应用及分类讨论的思想应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的一条渐近线与直线3x+$\sqrt{6}$y+3=0垂直,以C的右焦点F为圆心的圆(x-c)2+y2=2与它的渐近线相切,则双曲线的焦距为( )
| A. | 4 | B. | 2 | C. | $\sqrt{5}$ | D. | $2\sqrt{5}$ |
12.化简$\frac{1+sin8θ-cos8θ}{1+sin8θ+cos8θ}$等于( )
| A. | tan2θ | B. | cot4θ | C. | tan4θ | D. | cot2θ |
16.对于等比数列{an}的前n项和Sn( )
| A. | 任意一项都不为零 | B. | 必有一项为零 | ||
| C. | 至多有有限项为零 | D. | 可以有无数项为零 |
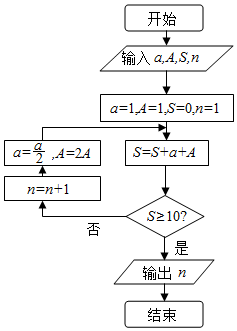 我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述,如图所示,则输出结果n=( )
我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述,如图所示,则输出结果n=( )