题目内容
3．不等式（3x+1）（1-2x）＞0的解集是（ ）| A． | $\{x|x＜-\frac{1}{3}或x＞\frac{1}{2}\}$ | B． | $\{x|-\frac{1}{3}＜x＜\frac{1}{2}\}$ | C． | $\{x|x＞\frac{1}{2}\}$ | D． | $\{x|x＞-\frac{1}{3}\}$ |
分析 把不等式化为（3x+1）（2x-1）＜0，求出解集即可．
解答 解：不等式（3x+1）（1-2x）＞0可化为
（3x+1）（2x-1）＜0，
解得-$\frac{1}{3}$＜x＜$\frac{1}{2}$，
∴不等式的解集是{x|-$\frac{1}{3}$＜x＜$\frac{1}{2}$}．
故选：B．
点评 本题考查了一元二次不等式的解法与应用问题，是基础题．
练习册系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
13．若$\sqrt{3}$是3a与3b的等比中项，则ab的最大值为（ ）
| A． | $\frac{1}{2}$ | B． | 0 | C． | $\frac{1}{4}$ | D． | 1 |
11．设随机变量X～N（100，σ），p（80＜X≤120）=$\frac{3}{4}$，则p（X＞120）=（ ）
| A． | $\frac{1}{16}$ | B． | $\frac{1}{8}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{2}$ |
8．若直线过点（1，2），（4，2+$\sqrt{3}$）则此直线的倾斜角是（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{2}$ |
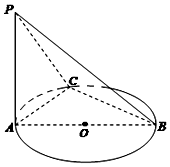如图，AB是⊙O的直径，PA垂直于⊙O所在平面，C是圆周上不同于A，B两点的任意一点，且AB=2，$PA=BC=\sqrt{3}$，则直线PC与底面ABC所成角的大小为（ ）