题目内容
10.已知函数f(x)=2x3+3x2+a,其中a∈R.(1)求函数f(x)的单调区间;
(2)若函数f(x)的图象与直线y=12x相切,求a的值;
(3)是否存在相异的正实数m,n,使得f(m)=12m,f(n)=12n?若存在,试确定实数a的取值范围;若不存在,说明理由.
分析 (1)求导数,利用导数的正负求函数f(x)的单调区间;
(2)若函数f(x)的图象与直线y=12x相切,求出切点坐标,即可求a的值;
(3)设F(x)=f(x)-12x,则题设可转化为判断函数F(x)在(0,+∞)上是否存在两个零点m,n.
解答 解:(1)f'(x)=6x2+6x=6x(x+1). (1分)
令f'(x)=0,得x1=-1,x2=0,列表如下:
| x | (-∞,-1) | -1 | (-1,0) | 0 | (0,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | 单调递增↗ | 极大值 | 单调递减↘ | 极小值 | 单调递增↗ |
(2)令f'(x)=12,即6x(x+1)=12,得x=-2或x=1. (5分)
∴切点坐标为(-2,-24)或(1,12). (6分)
将点(-2,-24)代入f(x)=2x3+3x2+a,得a=-20;
再将点(1,12)代入f(x)=2x3+3x2+a,得a=7. (7分)
故a=-20或a=7. (8分)
(3)设F(x)=f(x)-12x,
则题设可转化为判断函数F(x)在(0,+∞)上是否存在两个零点m,n.(*) (9分)
∵F(x)=f(x)-12x=2x3+3x2-12x+a,
∴F'(x)=6x2+6x-12=6(x+2)(x-1).
令F'(x)=0,得x1=-2,x2=1. (10分)
当0<x<1时,F'(x)<0;当x>1时,F'(x)>0.
故x=1是F(x)的极小值点,且F(1)=a-7. (11分)
要使(*)成立,则必有$\left\{\begin{array}{l}F(0)>0\\ F(1)<0\end{array}\right.$,即$\left\{\begin{array}{l}a>0\\ a-7<0\end{array}\right.$,
∴0<a<7,
此时F(2)=4+a>0,
故函数F(x)的图象与x轴的正半轴有两个交点(m,0),(n,0).
综上所述,存在相异的正实数m,n,使得f(m)=12m,f(n)=12n,
此时实数a的取值范围是{a|0<a<7}. (12分)
点评 本题考查导数知识的综合运用,考查导数的几何意义,考查函数的单调性,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
15.已知F是抛物线x2=y的焦点,A,B是该抛物线上的两点,|AF|+|BF|=3,则线段AB的中点到x轴的距离为( )
| A. | $\frac{3}{4}$ | B. | 1 | C. | $\frac{5}{4}$ | D. | $\frac{7}{4}$ |
20.在圆的方程x2+y2+Dx+Ey+F=0中,若D2=E2>4F,则圆的位置满足( )
| A. | 截两坐标轴所得弦的长度相等 | B. | 与两坐标轴都相切 | ||
| C. | 与两坐标轴相离 | D. | 上述情况都有可能 |

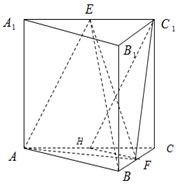 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB=AC,E,F,H分别是A1C1,BC,AC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB=AC,E,F,H分别是A1C1,BC,AC的中点. 如图,在三棱椎P-ABC中,D,E,F分别是棱PC、AC、AB的中点,且PA⊥面ABC.
如图,在三棱椎P-ABC中,D,E,F分别是棱PC、AC、AB的中点,且PA⊥面ABC.