题目内容
已知D,E,F分别是△ABC的三边BC,CA,AB上的点,且满足
=
,
=
,
=λ(
+
)(λ∈R),
•
=
•
,
=μ(
+
)(μ∈R).则
=( )
| AF |
| 2 |
| 3 |
| AB |
| AE |
| 3 |
| 4 |
| AC |
| AD |
| ||
|
|
| ||
|
|
| DE |
| DA |
| DE |
| DC |
| DF |
| ||
|
|
| ||
|
|
|
| ||
|
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:平面向量的综合题,平面向量数量积的运算
专题:平面向量及应用
分析:如图所示,由
=λ(
+
),可得
•
=0,得到BC⊥AD.由
•
=
•
,可得
•(
-
)=
•
=0,得到DE⊥CA.由
=μ(
+
),可得
•
=0,即BA⊥DF.连接EF.可得A,E,D,F四点共圆,因此∠AEF=∠ADF.又∠B=∠ADF,可得△AEF∽△ABC.又
=
,
=
,可得AC=
AB.即可得出
.
| AD |
| ||
|
|
| ||
|
|
| BC |
| AD |
| DE |
| DA |
| DE |
| DC |
| DE |
| DA |
| DC |
| DE |
| CA |
| DF |
| ||
|
|
| ||
|
|
| BA |
| DF |
| AF |
| 2 |
| 3 |
| AB |
| AE |
| 3 |
| 4 |
| AC |
2
| ||
| 3 |
|
| ||
|
|
解答:
解:如图所示,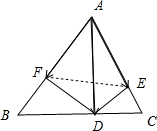
∵
=λ(
+
),
∴
•
=λ(
+
)•
=λ(
+
)=0,
∴
⊥
,即BC⊥AD.
∵
•
=
•
,∴
•(
-
)=
•
=0,∴
⊥
,即DE⊥CA.
∵
=μ(
+
),
∴
•
=μ(
+
)•
=μ(
+
)=0,
∴
⊥
,即BA⊥DF.
连接EF.
∵DE⊥AC,DF⊥AB,
∴A,E,D,F四点共圆,∴∠AEF=∠ADF.
又AD⊥BC,∴∠B=∠ADF,
∴∠B=∠AEF.
∴△AEF∽△ABC.
∴
=
=
.
∵
=
,
=
,
∴
=
,解得AC=
AB.
∴
=
=
.
∴
=
.
故选:D.

∵
| AD |
| ||
|
|
| ||
|
|
∴
| BC |
| AD |
| ||
|
|
| ||
|
|
| BC |
-|
| ||||
|
|
|
| ||||
|
|
∴
| BC |
| AD |
∵
| DE |
| DA |
| DE |
| DC |
| DE |
| DA |
| DC |
| DE |
| CA |
| DE |
| CA |
∵
| DF |
| ||
|
|
| ||
|
|
∴
| BA |
| DF |
| ||
|
|
| ||
|
|
| BA |
|
| ||||
|
|
-|
| ||||
|
|
∴
| BA |
| DF |
连接EF.
∵DE⊥AC,DF⊥AB,
∴A,E,D,F四点共圆,∴∠AEF=∠ADF.
又AD⊥BC,∴∠B=∠ADF,
∴∠B=∠AEF.
∴△AEF∽△ABC.
∴
| EF |
| BC |
| AE |
| AB |
| AF |
| AC |
∵
| AF |
| 2 |
| 3 |
| AB |
| AE |
| 3 |
| 4 |
| AC |
∴
| ||
| AB |
| ||
| AC |
2
| ||
| 3 |
∴
| EF |
| BC |
| ||||||
| AB |
| ||
| 2 |
∴
|
| ||
|
|
| ||
| 2 |
故选:D.
点评:本题考查了向量垂直与数量积的关系、四点共圆的判定与性质、相似三角形的判定与性质、向量共线定理等基础知识与基本技能方法,考查了分析问题和解决问题的能力,考查了推理能力和计算能力,属于难题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
“已知实数x,y满足(x-1)2+(y-1)2=1,求
的最大值”时,可理解为在以点(1,1)为圆心,以1为半径的圆上找一点,使它到原点距离最远问题,据此类比到空间,试分析:已知实数x,y,z满足(x-1)2+(y-1)2+(z-1)2=1,求
的最大值是( )
| x2+y2 |
| x2+y2+z2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
执行如图所示程序框图,输出的x值为( )


| A、11 | B、13 | C、15 | D、4 |
四棱锥P-ABCD的顶点P在底面ABCD的投影恰好是点A,三视图如图所示,则此四棱锥的表面积为( )


| A、2 | ||
| B、3 | ||
C、2+
| ||
D、3+
|