题目内容
9．某班级有50名同学，一次数学测试平均成绩是92，如果学号为1号到30号的同学平均成绩为90，则学号为31号到50号同学的平均成绩为95．分析 设学号为31号到50号同学的平均成绩为x，得到关于x的方程，解出即可．
解答 解：设学号为31号到50号同学的平均成绩为x，
则92×50=90×30+20x，解得：x=95，
故答案为：95．
点评 本题考查了平均数问题，掌握平均数的定义是解题的关键，本题是一道基础题．
练习册系列答案
阅读快车系列答案
相关题目
19．连续两次抛掷一枚骰子，记录向上的点数，则向上的点数之差的绝对值为2的概率是（ ）
| A． | $\frac{1}{9}$ | B． | $\frac{2}{9}$ | C． | $\frac{4}{9}$ | D． | $\frac{1}{3}$ |
4．若关于x的方程2sin（2x+$\frac{π}{6}$）=m在[0，$\frac{π}{2}$]上有两个不等实根，则m的取值范围是（ ）
| A． | （1，$\sqrt{3}$） | B． | [0，2] | C． | [1，2） | D． | [1，$\sqrt{3}$] |
18．设函数f（x）=$\left\{\begin{array}{l}{{e}^{x}，0≤x＜1}\\{lnx+e，1≤x≤e}\end{array}\right.$在区间[0，e]上随机取一个实数x，则f（x）的值不小于常数e的概率是（ ）
| A． | $\frac{1}{e}$ | B． | 1-$\frac{1}{e}$ | C． | $\frac{e}{1+e}$ | D． | $\frac{1}{1+e}$ |
19．
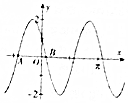已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的图象如图所示，其中A（-$\frac{5π}{12}$，0），B（$\frac{π}{12}$，0），则函数f（x）的单调增区间为（ ）
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的图象如图所示，其中A（-$\frac{5π}{12}$，0），B（$\frac{π}{12}$，0），则函数f（x）的单调增区间为（ ）| A． | [-$\frac{π}{6}$+kπ，$\frac{π}{3}$+kπ]（k∈Z） | B． | [$\frac{π}{3}$+kπ，$\frac{5π}{6}$+kπ]（k∈Z） | ||
| C． | [-$\frac{π}{6}$+2kπ，$\frac{π}{3}$+2kπ]（k∈Z） | D． | [$\frac{π}{3}$+2kπ，$\frac{5π}{6}$+2kπ]（k∈Z） |