题目内容
14.已知点M是圆心为E的圆(x+$\sqrt{3}$)2+y2=16上的动点,点F($\sqrt{3}$,0),线段MF的垂直平分线交EM于点P.(Ⅰ)求动点P的轨迹C的方程;
(Ⅱ)过原点O作直线l交(Ⅰ)中的轨迹C于点A,B,点D满足$\overrightarrow{FD}$=$\overrightarrow{FA}$+$\overrightarrow{FB}$,试求四边形AFBD的面积的取值范围.
分析 (Ⅰ)得到|PM|=|PF|,求出点P的轨迹是椭圆,其中2a=4,c=$\sqrt{3}$,求出椭圆方程即可;
(Ⅱ)求出SAFBD=2S△AFB,通过讨论AB是短轴、AB是长轴的情况,求出四边形的面积即可.
解答 解:(Ⅰ)由于点P为线段MF的垂直平分线,
故|PM|=|PF|,
故|PE|+|PF|=|PE|+|PM|=|ME|=4>2$\sqrt{3}$,
故点P的轨迹是椭圆,其中2a=4,c=$\sqrt{3}$,
因此P点的轨迹C的方程是:$\frac{{x}^{2}}{4}$+y2=1;
(Ⅱ)由$\overrightarrow{FD}$=$\overrightarrow{FA}$+$\overrightarrow{FB}$,知四边形AFBD是平行四边形,
故SAFBD=2S△AFB,
(1)AB是短轴时,
S△AFB=$\frac{1}{2}$|AB|•|OF|=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$
即SAFBD=2$\sqrt{3}$;
(2)AB是长轴时,易知AFBD不是四边形,故AB斜率不是0;
(3)直线AB的斜率存在且不是0时,设其斜率为k,
则直线AB的方程是:y=kx(k≠0),
设A(x1,y1),B(x2,y2),
联立方程组$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}{+y}^{2}=1}\\{y=kx}\end{array}\right.$,消去x得:
(1+4k2)y2-4k2=0,
故y1+y2=0,y1y2=$\frac{-{4k}^{2}}{1+{4k}^{2}}$,
SAFBD=2S△ABF=2×$\frac{1}{2}$|OF|•|y1-y2|=$\sqrt{3}$•$\sqrt{{{(y}_{1}{+y}_{2})}^{2}-{{4y}_{1}y}_{2}}$=$\sqrt{3}$•$\sqrt{\frac{1{6k}^{2}}{1+{4k}^{2}}}$=$\frac{4\sqrt{3}}{\sqrt{\frac{1}{{k}^{2}}+4}}$,
而$\frac{1}{{k}^{2}}$+4>4,故0<$\frac{4\sqrt{3}}{\sqrt{\frac{1}{{k}^{2}}+4}}$<$\frac{4\sqrt{3}}{\sqrt{4}}$=2$\sqrt{3}$,
综上,四边形AFBD的面积的取值范围是(0,2$\sqrt{3}$].
点评 本题考查了椭圆的轨迹方程,考查分类讨论思想以及转化思想,是一道中档题.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案| A. | (1,$\sqrt{3}$) | B. | [0,2] | C. | [1,2) | D. | [1,$\sqrt{3}$] |
| A. | $[\sqrt{5},2\sqrt{5}]$ | B. | $[\sqrt{5},2\sqrt{10})$ | C. | $(\sqrt{5},\sqrt{10})$ | D. | $[\sqrt{5},2\sqrt{10}]$ |
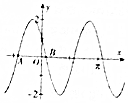 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,其中A(-$\frac{5π}{12}$,0),B($\frac{π}{12}$,0),则函数f(x)的单调增区间为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,其中A(-$\frac{5π}{12}$,0),B($\frac{π}{12}$,0),则函数f(x)的单调增区间为( )| A. | [-$\frac{π}{6}$+kπ,$\frac{π}{3}$+kπ](k∈Z) | B. | [$\frac{π}{3}$+kπ,$\frac{5π}{6}$+kπ](k∈Z) | ||
| C. | [-$\frac{π}{6}$+2kπ,$\frac{π}{3}$+2kπ](k∈Z) | D. | [$\frac{π}{3}$+2kπ,$\frac{5π}{6}$+2kπ](k∈Z) |
 每年的4月23日为世界读书日,为调查某高校学生(学生很多)的读书情况,随机抽取了男生,女生各20人组成的一个样本,对他们的年阅读量(单位:本)进行了统计,分析得到了男生年阅读量的频率分布表和女生阅读量的频率分布直方图.
每年的4月23日为世界读书日,为调查某高校学生(学生很多)的读书情况,随机抽取了男生,女生各20人组成的一个样本,对他们的年阅读量(单位:本)进行了统计,分析得到了男生年阅读量的频率分布表和女生阅读量的频率分布直方图.男生年阅读量的频率分布表(年阅读量均在区间[0,60]内):
| 本/年 | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60] |
| 频数 | 3 | 1 | 8 | 4 | 2 | 2 |
(Ⅱ)在样本中,利用分层抽样的方法,从男生年与度量在[20,30),[30,40)的两组里抽取6人,再从这6人中随机抽取2人,求[30,40)这一组中至少有1人被抽中的概率;
(Ⅲ)若年阅读量不小于40本为阅读丰富,否则为阅读不丰富,依据上述样本研究阅读丰富与性别的关系,完成下列2×2列联表,并判断是否有99%的把握认为月底丰富与性别有关.
| 性别 阅读量 | 丰富 | 不丰富 | 合计 |
| 男 | |||
| 女 | |||
| 合计 |
| P(K2≥k0) | 0.025 | 0.010 | 0.005 |
| k0 | 5.024 | 6.635 | 7.879 |
| A. | {8,10} | B. | {8,12} | C. | {8,14} | D. | {8,10,14} |
| A. | 10-ln3 | B. | 8-ln3 | C. | $\frac{22}{3}$ | D. | $\frac{64}{9}$ |