题目内容
4.若将一个45°的直角三角板的一直角边放在一桌面上,另一直角边与桌面所成角为45°,则此时该三角板的斜边与桌面所成的角等于30°.分析 直角三角形ABC中,∠ABC=90°,AB=BC,BC?平面α,AO⊥α,交α于O,∠PBO=45°,此时该三角板的斜边与桌面所成的角为∠ACO,由此能求出该三角板的斜边与桌面所成的角.
解答 解: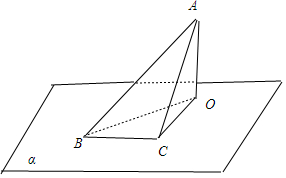 如图,直角三角形ABC中,∠ABC=90°,AB=BC,
如图,直角三角形ABC中,∠ABC=90°,AB=BC,
BC?平面α,AO⊥α,交α于O,∠PBO=45°,
此时该三角板的斜边与桌面所成的角为∠ACO,
设AB=BC=1,则AC=$\sqrt{2}$,AO=BC=$\sqrt{\frac{1}{2}}$=$\frac{\sqrt{2}}{2}$,
∴sin$∠ACO=\frac{AO}{AC}$=$\frac{1}{2}$,
∴∠ACO=30°.
∴该三角板的斜边与桌面所成的角等于30°.
故答案为:30°.
点评 本题考查线面角的求不地,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
9.现有如下的错误推理:“因为任何复数的平方都大于等于0,而i是复数,所以i2>0,即-1>0”,其错误的原因是( )
| A. | 大前提错误导致结论错误 | B. | 小前提错误导致结论错误 | ||
| C. | 推理形式错误导致结论错误 | D. | 大前提和推理形式都错误导致错误 |
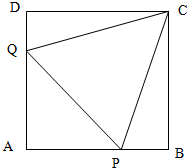 如图,正方形ABCD的边长为1,P,Q分别为边AB,DA上的点,且都不与A,B,D重合,线段PQ的长为1,△CPQ的面积用y表示.
如图,正方形ABCD的边长为1,P,Q分别为边AB,DA上的点,且都不与A,B,D重合,线段PQ的长为1,△CPQ的面积用y表示.