题目内容
13.若直线ax+2by-2=0(a,b>0)始终平分圆x2+y2-4x-2y=0的周长,则$\frac{1}{a}$+$\frac{2}{b}$的最小值为3+2$\sqrt{2}$.分析 由题意得,直线过圆心(2,1),即 a+b=1,$\frac{1}{a}$+$\frac{2}{b}$=(a+b)($\frac{1}{a}$+$\frac{2}{b}$)=3+$\frac{b}{a}$+$\frac{2a}{b}$,利用基本不等式求出其最小值.
解答 解:由题意得,直线过圆心(2,1),所以,a+b=1.
∴$\frac{1}{a}$+$\frac{2}{b}$=(a+b)($\frac{1}{a}$+$\frac{2}{b}$)=3+$\frac{b}{a}$+$\frac{2a}{b}$≥3+2$\sqrt{2}$,当且仅当$\frac{b}{a}$=$\frac{2a}{b}$时,等号成立,
故答案为3+2$\sqrt{2}$.
点评 本题考查直线和圆相交的性质,基本不等式的应用,解题的突破口是判断直线过圆心,解题的关键是利用a+b=1.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
1.对于R上可导的任意函数f(x),若满足$\frac{3+2x}{f′(x)}$≥0,则有( )
| A. | f(-1)+f(-2)<2f(-$\frac{3}{2}$) | B. | f(-1)+f(-2)>2f(-$\frac{3}{2}$) | C. | f(-1)+f(-2)≤2f(-$\frac{3}{2}$) | D. | f(-1)+f(-2)≥2f(-$\frac{3}{2}$) |
18.已知函数f(x)=x3-6x2+12x+a(a∈R),则函数f(x)的极值点的个数为( )
| A. | 0 | B. | 1 | ||
| C. | 2 | D. | 与实数a的取值有关 |
3.某校在高二文理分科时,随机调查了该校高二的一些学生,得到数据如表:
为了检验科类与数学是否优秀有关系,根据表中的数据,得到K2≈4.84.因为K2>3.841,所以断定科类与数学是否优秀有关系,这种判断出错的概率不超过0.05.
| 文科 | 理科 | |
| 数学优秀 | 10 | 13 |
| 数学不优秀 | 20 | 7 |
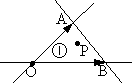 如图,已知O,A,B是平面内不共线的三点,且$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,直线OA,OB,AB将平面区域分成7部分,若点P落在区域①中(含边界),则z=2x+y的最大值为( )
如图,已知O,A,B是平面内不共线的三点,且$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,直线OA,OB,AB将平面区域分成7部分,若点P落在区域①中(含边界),则z=2x+y的最大值为( )