题目内容
双曲线的实轴和虚轴的4个端点都在一圆上，则此双曲线两渐近线的夹角为（ ）
| A、30° | B、45° |
| C、60° | D、90° |
考点：双曲线的简单性质
专题：计算题,直线与圆,圆锥曲线的定义、性质与方程
分析：由已知可得a=b，进而得到渐近线方程，由两直线垂直的条件，进而得到夹角．
解答：
解：双曲线的实轴和虚轴的4个端点都在一圆上，
则a=b，即为等轴双曲线，
则渐近线方程为y=±x，
则它们垂直，故夹角为90°．
故选：D．
则a=b，即为等轴双曲线，
则渐近线方程为y=±x，
则它们垂直，故夹角为90°．
故选：D．
点评：本题考查双曲线的性质，考查两直线垂直的条件，考查运算能力，属于基础题．
练习册系列答案
相关题目
命题“?x∈R，x2-3x+2≥0”的否定是（ ）
| A、?x0∈R，x02-3x0+2＜0 |
| B、?x0∈R，x02-3x0+2≥0 |
| C、?x0∉R，x02-3x0+2＜0 |
| D、?x0∈R，x02-3x0+2＜0 |
假设某设备的使用年限x（年）和所支出的维修费用y（元）呈线性相关关系，且有如下的统计资料：
则x和y之间的线性回归方程为（ ）
| 使用年限x（年） | 2 | 3 | 4 | 5 | 6 |
| 维修费用y（元） | 2.2 | 3.8 | 5.5 | 6.5 | 7 |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f（x）=sin（ωx+φ），其中ω＞0，|φ|＜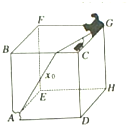
一位电脑爱好者设计了一个“猫捉老鼠”的动画游戏，如图所示，在一个边长为a的大正方体木箱的一个顶点G上，老鼠从猫的爪间逃出，沿着木箱的棱边奔向洞口，洞口子在方木箱的另一顶点A处，若老鼠在奔跑中，并不重复跳过任意一条棱边，也不再回到G点，聪明的猫也选择了一条最短的路程奔向洞口（设猫和老鼠同时从G点出发），结果猫再次在洞口A捉住了老鼠，问：