题目内容
 函数f(x)=sin(ωx+φ),其中ω>0,|φ|<
函数f(x)=sin(ωx+φ),其中ω>0,|φ|<| π |
| 2 |
(1)求函数f(x)的解析式;
(2)写出f(x)的最值及相应的x的取值构成的集合.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:(1)利用图象的最低点确定A的值,利用周期确定ω,再根据图象过点(
,0),确定φ的值,即可求函数f(x)的解析式;
(2)由2x+
=2kπ+
,k∈Z,2x+
=2kπ+
,k∈Z,即可解得f(x)的最值及相应的x的取值构成的集合.
| π |
| 3 |
(2)由2x+
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
解答:
解:(1)由题意,函数的最小值为-1,∴A=1,
∵T=4×(
π-
)=π,
∴ω=2,
∴f(x)=sin(2x+φ),
∵图象过点(
,0),
∴sin(2×
+φ)=0,
∵|φ|<
,∴φ=
∴f(x)=sin(2x+
);
(2)当2x+
=2kπ+
,k∈Z,即有x∈{x|x=kπ+
,k∈Z}时,f(x)max=1;
当2x+
=2kπ+
,k∈Z,即有x∈{x|x=kπ+
,k∈Z}时,f(x)min=-1.
∵T=4×(
| 7 |
| 12 |
| π |
| 3 |
∴ω=2,
∴f(x)=sin(2x+φ),
∵图象过点(
| π |
| 3 |
∴sin(2×
| π |
| 3 |
∵|φ|<
| π |
| 2 |
| π |
| 3 |
∴f(x)=sin(2x+
| π |
| 3 |
(2)当2x+
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
当2x+
| π |
| 3 |
| 3π |
| 2 |
| 7π |
| 12 |
点评:本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的图象和性质,属于基础题.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
已知f(ex)=x,则f(5)=( )
| A、ln5 |
| B、lg5 |
| C、e5 |
| D、5e |
下列说法正确的是( )
| A、数列2,3,4与数列4,3,2是同一数列 | ||||
| B、数列1,2,3与数列1,2,3,…是同一数列 | ||||
C、1,4,2,
| ||||
| D、数列{2n-3}与-1,1,3,5,…不一定是同一数列 |
双曲线的实轴和虚轴的4个端点都在一圆上,则此双曲线两渐近线的夹角为( )
| A、30° | B、45° |
| C、60° | D、90° |
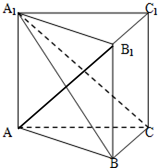 如图,在直三棱柱ABC-A1B1C1(侧棱垂直于底面)中,BC⊥AB,且AA1=AB=2.
如图,在直三棱柱ABC-A1B1C1(侧棱垂直于底面)中,BC⊥AB,且AA1=AB=2.