题目内容
15.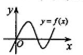 设函数y=f(x)在定义域内可导,其图象如图所示,则导函数y=f′(x)的图象只可能是下列情形中的( )
设函数y=f(x)在定义域内可导,其图象如图所示,则导函数y=f′(x)的图象只可能是下列情形中的( )| A. | 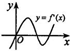 | B. | 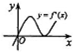 | C. | 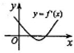 | D. | 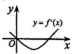 |
分析 由导数的正负与函数的单调性的关系可判断当x∈(-∞,a),(b,+∞)时,y=f′(x)>0,当x∈(a,b)时,y=f′(x)<0,从而确定答案.
解答 解:∵导数的正负确定了函数的单调性,
∴从函数f(x)的图象可知,
y=f(x)在(-∞,a),(b,+∞)上单调递增,
在(a,b)上单调递减;
a,b是函数y=f(x)的极值点;
故当x∈(-∞,a),(b,+∞)时,y=f′(x)>0,
当x∈(a,b)时,y=f′(x)<0,
故选C.
点评 本题考查了导数的应用及数形结合的思想应用.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
6.sin20°cos170°-cos20°sin10°=( )
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
10.下列函数求导运算正确的有( )
①(3x)′=3xlog3e;
②(log2x)′=$\frac{1}{xln2}$;
③(ex)′=ex;
④($\frac{1}{lnx}$)′=x;
⑤(x•ex)=ex(1+x)
①(3x)′=3xlog3e;
②(log2x)′=$\frac{1}{xln2}$;
③(ex)′=ex;
④($\frac{1}{lnx}$)′=x;
⑤(x•ex)=ex(1+x)
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.设集合A={x|-5<x<3},集合B=N,则A∩B=( )
| A. | {1,2} | B. | {0,1,2} | C. | {1,2,3} | D. | {0,1,2,3} |
4.-$\int{\begin{array}{l}2\\ 1\end{array}}$xdx=( )
| A. | $-\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | -1 | D. | 1 |