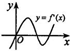题目内容
4.-$\int{\begin{array}{l}2\\ 1\end{array}}$xdx=( )| A. | $-\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | -1 | D. | 1 |
分析 求出被积函数的原函数,利用微积分基本定理求值.
解答 解:-$\int{\begin{array}{l}2\\ 1\end{array}}$xdx=-$\frac{1}{2}{x}^{2}$|${\;}_{1}^{2}$=$-\frac{3}{2}$;
故选A.
点评 本题考查了定积分的计算;关键是正确找出原函数.

练习册系列答案
相关题目
14.设f(x)是定义在R上的奇函数,f(x)+f(2+x)=0,当x∈[0,2]时,f(x)=(x-1)2-1,若关于x的方程f(x)-k(x-1)=0恰有三个不同的实数解,则正实数k的取值范围为( )
| A. | ($\sqrt{3}$-$\sqrt{2}$,4-$\sqrt{13}$) | B. | (8-2$\sqrt{15}$,4-$\sqrt{13}$) | C. | (5-2$\sqrt{6}$,4-2$\sqrt{3}$) | D. | (8-2$\sqrt{15}$,4-2$\sqrt{3}$) |
16.设集合M=$\left\{{\left.x\right|x=tan\frac{π}{4}}\right\}$,N=$\left\{{\frac{1}{2},\frac{{\sqrt{2}}}{2},\frac{{\sqrt{3}}}{2},\sqrt{3}}\right\}$,则M∩N=( )
| A. | M | B. | $\left\{{\frac{{\sqrt{2}}}{2}}\right\}$ | C. | ∅ | D. | {0} |
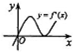
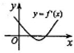
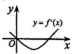
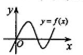 设函数y=f(x)在定义域内可导,其图象如图所示,则导函数y=f′(x)的图象只可能是下列情形中的( )
设函数y=f(x)在定义域内可导,其图象如图所示,则导函数y=f′(x)的图象只可能是下列情形中的( )