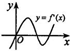题目内容
3．函数y=$\sqrt{\sqrt{3}tanx-3}$的定义域为$\{x|kπ+\frac{π}{3}≤x＜kπ+\frac{π}{2}，k∈Z\}$．分析 根据二次根式以及三角函数的性质求出x的范围即可．
解答 解：由题意得：$\sqrt{3}$tanx-3≥0，
解得：$\{x|kπ+\frac{π}{3}≤x＜kπ+\frac{π}{2}，k∈Z\}$，
故答案为：$\{x|kπ+\frac{π}{3}≤x＜kπ+\frac{π}{2}，k∈Z\}$．
点评 本题考查了二次根式以及三角函数的性质，是一道基础题．
练习册系列答案
阅读快车系列答案
相关题目
14．设f（x）是定义在R上的奇函数，f（x）+f（2+x）=0，当x∈[0，2]时，f（x）=（x-1）2-1，若关于x的方程f（x）-k（x-1）=0恰有三个不同的实数解，则正实数k的取值范围为（ ）
| A． | （$\sqrt{3}$-$\sqrt{2}$，4-$\sqrt{13}$） | B． | （8-2$\sqrt{15}$，4-$\sqrt{13}$） | C． | （5-2$\sqrt{6}$，4-2$\sqrt{3}$） | D． | （8-2$\sqrt{15}$，4-2$\sqrt{3}$） |
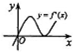
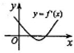
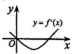
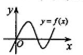设函数y=f（x）在定义域内可导，其图象如图所示，则导函数y=f′（x）的图象只可能是下列情形中的（ ）
