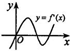题目内容
5.已知$\overrightarrow a=(3,2),\;\overrightarrow b=({-1,2}),\overrightarrow c=({4,1})$,若$(\overrightarrow a+k\overrightarrow c)∥(2\overrightarrow b-\overrightarrow a)k$,则实数k的值-$\frac{16}{13}$或0,若$(\overrightarrow a+k\overrightarrow c)⊥(2\overrightarrow b-\overrightarrow a)k$,则实数k的值$-\frac{11}{18}$或0.分析 直接利用向量求解共线向量,利用共线向量平行于垂直的充要条件列出方程求解即可.
解答 解:$\overrightarrow a=(3,2),\;\overrightarrow b=({-1,2}),\overrightarrow c=({4,1})$,可得$\overrightarrow{a}+k\overrightarrow{c}$=(3+4k,2+k).$(2\overrightarrow{b}-\overrightarrow{a})k$=(-5k,2k)
若$(\overrightarrow a+k\overrightarrow c)∥(2\overrightarrow b-\overrightarrow a)k$,可得-5k(2+k)=2k(3+4k),解得k=-$\frac{16}{13}$,或k=0.
若$(\overrightarrow a+k\overrightarrow c)⊥(2\overrightarrow b-\overrightarrow a)k$,可得-5k(3+4k)+2k(2+k)=0.
则实数k=$-\frac{11}{18}$,或k=0.
故答案为:-$\frac{16}{13}$或0;$-\frac{11}{18}$或0.
点评 本题考查向量的共线与垂直的应用,考查计算能力.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案
相关题目
17.设定义域为R的函数f(x)=$\left\{\begin{array}{l}{{2}^{-|x-1|}+1,(x≠1)}\\{a,(x=1)}\end{array}\right.$,若关于x的方程2f2(x)-(2a+3)f(x)+3a=0有五个不同的实数解,则a的取值范围是( )
| A. | (0,1) | B. | $(0,\frac{3}{2})$ | C. | (1,2) | D. | $(1,\frac{3}{2})∪$$(\frac{3}{2},2)$ |
14.设f(x)是定义在R上的奇函数,f(x)+f(2+x)=0,当x∈[0,2]时,f(x)=(x-1)2-1,若关于x的方程f(x)-k(x-1)=0恰有三个不同的实数解,则正实数k的取值范围为( )
| A. | ($\sqrt{3}$-$\sqrt{2}$,4-$\sqrt{13}$) | B. | (8-2$\sqrt{15}$,4-$\sqrt{13}$) | C. | (5-2$\sqrt{6}$,4-2$\sqrt{3}$) | D. | (8-2$\sqrt{15}$,4-2$\sqrt{3}$) |
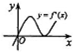
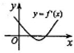
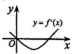
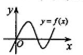 设函数y=f(x)在定义域内可导,其图象如图所示,则导函数y=f′(x)的图象只可能是下列情形中的( )
设函数y=f(x)在定义域内可导,其图象如图所示,则导函数y=f′(x)的图象只可能是下列情形中的( )