题目内容
11.在△ABC中,已知D是AB边上一点,若$\overrightarrow{AD}$=$\frac{1}{3}\overrightarrow{AB}$,$\overrightarrow{CD}$=$\frac{2}{3}$$\overrightarrow{CA}$+$λ\overrightarrow{CB}$,则λ=( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | -$\frac{1}{3}$ | D. | -$\frac{2}{3}$ |
分析 可作出图形,由条件$\overrightarrow{AD}=\frac{1}{3}\overrightarrow{AB}$及向量加法和减法的几何意义,以及向量的数乘运算便可以得出$\overrightarrow{CD}=\frac{2}{3}\overrightarrow{CA}+\frac{1}{3}\overrightarrow{CB}$,这样根据平面向量基本定理即可得出λ的值.
解答 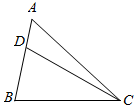 解:如图,
解:如图,
$\overrightarrow{CD}=\overrightarrow{CA}+\overrightarrow{AD}$=$\overrightarrow{CA}+\frac{1}{3}\overrightarrow{AB}$=$\overrightarrow{CA}+\frac{1}{3}(\overrightarrow{CB}-\overrightarrow{CA})$=$\frac{2}{3}\overrightarrow{CA}+\frac{1}{3}\overrightarrow{CB}$;
又$\overrightarrow{CD}=\frac{2}{3}\overrightarrow{CA}+λ\overrightarrow{CB}$;
∴由平面向量基本定理得,$λ=\frac{1}{3}$.
故选:B.
点评 考查向量加法和减法的几何意义,以及向量的数乘运算,平面向量基本定理.

练习册系列答案
相关题目
19.若向量$\overrightarrow{a}$、$\overrightarrow{b}$满足|$\overrightarrow{a}$|=|2$\overrightarrow{a}$+$\overrightarrow{b}$|=2,则$\overrightarrow{a}$在$\overrightarrow{b}$方向上投影的最大值是( )
| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | $\sqrt{6}$ | D. | -$\sqrt{6}$ |



