题目内容
17.若函数$f(x)={x^{\frac{2}{3}}}$,则f(x)的图象为( )| A. |  | B. |  | ||
| C. |  | D. |  |
分析 先判断奇偶性,再判断函数的变化趋势,即可判断.
解答 解:f(-x)=$(-x)^{\frac{2}{3}}$=${x}^{\frac{2}{3}}$=f(x),
所以函数f(x)为偶函数,故图象关于y轴对称,故排除B,D,
由f′(x)=$\frac{2}{3}{x}^{-\frac{1}{3}}$,
当x>0时,f′(x)为减函数,
故f(x)的切线的斜率越来越小,
故f(x)增加的越来越慢,
故选:A.
点评 本题考查了函数的图象识别,关键是掌握函数的单调性以及函数的变化趋势,属于基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
11.在△ABC中,已知D是AB边上一点,若$\overrightarrow{AD}$=$\frac{1}{3}\overrightarrow{AB}$,$\overrightarrow{CD}$=$\frac{2}{3}$$\overrightarrow{CA}$+$λ\overrightarrow{CB}$,则λ=( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | -$\frac{1}{3}$ | D. | -$\frac{2}{3}$ |
5.已知圆x2+y2=9与圆x2+y2-4x+4y-1=0关于直线l对称,则直线l的方程是( )
| A. | x-y+1=0 | B. | x-y-2=0 | C. | 3x-2y+1=0 | D. | x+y-1=0 |
12.直线l1:4x+3y-1=0与直线l2:8x+6y+3=0的距离为( )
| A. | $\frac{2}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
9.已知函数f(x)=3x+x-5,用二分法求方程3x+x-5=0在x∈(0,2)内近似解的过程中,取区间中点x0=1,那么下一个有根区间为( )
| A. | (0,1) | B. | (1,2) | C. | (1,2)或(0,1)都可以 | D. | 不能确定 |
6.设复数z=(7+3i)i2(i为虚数单位)在复平面上对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.执行如图的程序框图,则输出的S=( )
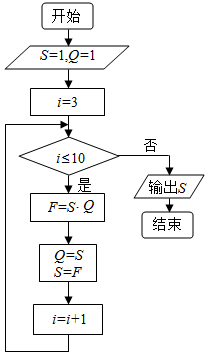

| A. | 21 | B. | 34 | C. | 55 | D. | 89 |