题目内容
已知lg(x-y)+lg(x+y)=lg2+lgx+lgy.求
的值.
| x |
| y |
考点:对数的运算性质
专题:函数的性质及应用
分析:利用对数的运算法则可得(x-y)(x+y)=2xy,
>1.化为(
)2-2•
-1=0,解出即可.
| x |
| y |
| x |
| y |
| x |
| y |
解答:
解:∵lg(x-y)+lg(x+y)=lg2+lgx+lgy.x-y>0,x+y>0,x,y>0.
∴lg[(x-y)(x+y)]=lg(2xy),
>1.
∴(x-y)(x+y)=2xy,
化为(
)2-2•
-1=0,
解得
=
=1±
,
又
>1,
∴
=1+
.
∴lg[(x-y)(x+y)]=lg(2xy),
| x |
| y |
∴(x-y)(x+y)=2xy,
化为(
| x |
| y |
| x |
| y |
解得
| x |
| y |
2±2
| ||
| 2 |
| 2 |
又
| x |
| y |
∴
| x |
| y |
| 2 |
点评:本题考查了对数的运算法则、一元二次方程的解法,属于基础题.

练习册系列答案
相关题目
一物体的运动方程为s=
+2t(t>1),其中s的单位是米,t的单位是秒,那么物体在2秒末的瞬时速度是( )
| 1 |
| t |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知直线ax+y+2=0的倾斜角为
,则a等于( )
| 3π |
| 4 |
| A、1 | ||
| B、-1 | ||
C、
| ||
| D、-2 |
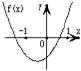 函数f(x)=(x-a)(x-b)(其中a>b)的图象如图所示,则函数g(x)=ax+b的大致图象是( )
函数f(x)=(x-a)(x-b)(其中a>b)的图象如图所示,则函数g(x)=ax+b的大致图象是( )