题目内容
15.若集合{1,$\frac{b}{a}$,a}={0,a+b,a2},则a2+b2=( )| A. | -1 | B. | 1 | C. | 0 | D. | ±1 |
分析 根据题意,集合{1,$\frac{b}{a}$,a}={0,a+b,a2},注意到后面集合中有元素0,由集合相等的意义,结合集合中元素的特征,可得b=0,进而分析可得a的值,计算可得答案.
解答 解:根据题意,集合{1,$\frac{b}{a}$,a}={0,a+b,a2},
又∵a≠0,
∴$\frac{b}{a}=0$,即b=0.
此时{1,0,a}={0,a,a2},
则a2=1,a=-1(舍去a=1).
∴则a2+b2=1.
故选:B.
点评 本题考查集合元素的特征与集合相等的含义,注意从特殊元素下手,有利于找到解题切入点,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.已知a,b,c∈R,且ac=b2,a+b+c=3,则b的取值范围是( )
| A. | [0,1] | B. | [-3,-1] | C. | [-1,1] | D. | [-3,1] |
20.$\root{3}{-27}$等于( )
| A. | 3 | B. | -3 | C. | ±3 | D. | -27 |
7.若直线L1:x+ay+6=0与直线L2:(a-2)x+3y+2a=0互相平行,则a的值为( )
| A. | -1或3 | B. | 1或3 | C. | -1 | D. | 以上都不对 |
4.已知奇函数f(x)在(0,+∞)上是增函数,且f(2)=0,则f(x)>0的解集为( )
| A. | (0,2) | B. | (-2,0) | C. | (-2,0)∪(2,+∞) | D. | (-2,2) |
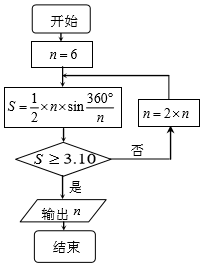 公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”,利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出的值为( )(参考数据:sin15°=0.2588,sin7.5°=0.1305)
公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”,利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出的值为( )(参考数据:sin15°=0.2588,sin7.5°=0.1305)