题目内容
曲线y=x3+x-2上点P0处的切线斜率为4，则点P0的一个坐标是（ ）
| A、（0，-2） |
| B、（1，1） |
| C、（-1，-4） |
| D、（1，4） |
考点：导数的几何意义
专题：导数的综合应用
分析：求出函数的导数，利用导数的几何意义，即可求出切点的坐标．
解答：
解：∵y=f（x）=x3+x-2，
∴f′（x）=3x2+1，
∵曲线y=x3+x-2上点P0处的切线斜率为4，
∴由f′（x）=3x2+1=4，
即x2=1，解得x=±1，
则f（1）=1+1-2=0，f（-1）=-1-1-2=-4，
则点P0的一个坐标为（1，0）或（-1，-4），
故选：C
∴f′（x）=3x2+1，
∵曲线y=x3+x-2上点P0处的切线斜率为4，
∴由f′（x）=3x2+1=4，
即x2=1，解得x=±1，
则f（1）=1+1-2=0，f（-1）=-1-1-2=-4，
则点P0的一个坐标为（1，0）或（-1，-4），
故选：C
点评：本题主要考查导数的几何意义，利用函数的导数是切线的斜率是解决本题的关键．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
已知向量
=（k，1），
=（2，-2），如果
∥
，那么（ ）
| a |
| b |
| a |
| b |
A、k=1且
| ||||
B、k=1且
| ||||
C、k=-1且
| ||||
D、k=-1且
|
下列函数中，导函数是奇函数的是（ ）
| A、y=sinx | ||
| B、y=ex | ||
| C、y=lnx | ||
D、y=cosx-
|
乒乓球运动员10人，其中男女运动员各5人，从这10名运动员中选出4人进行男女混合双打比赛，选法种数为（ ）
A、（A
| ||||
B、（C
| ||||
C、（C
| ||||
D、（C
|
用”辗转相除法”求得98与63的最大公约数是（ ）
| A、17 | B、14 | C、9 | D、7 |
已知向量
=（0，1），
=（1，0），
=（3，4），若λ为实数，且（
+λ
）⊥
，则λ的值为（ ）
| a |
| b |
| c |
| b |
| a |
| c |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
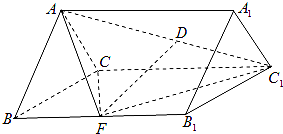如图，正三棱柱ABC-A1B1C1的各棱长都等于2，D在AC1上，F为BB1中点，且FD⊥AC1．
如图，四棱柱ABCD-A1B1C1D1中，平面A1ABB1⊥平面ABCD，且∠ABC=