题目内容
在四边形ABCD中,AD∥BC,AC⊥BD,已知
=6
+
,
=x
+y
,
=-2
-3
,(
,
这分别是x,y轴上方的单位向量),求x,y(x,y∈R)的值.
| AB |
| i |
| j |
| BC |
| i |
| j |
| CD |
| i |
| j |
| i |
| j |
考点:向量在几何中的应用
专题:计算题,平面向量及应用
分析:由题意,利用坐标表示向量
=6
+
=(6,1),
=x
+y
=(x,y),
=-2
-3
=(-2,-3),从而表示出
,
,
等向量,从而求值.
| AB |
| i |
| j |
| BC |
| i |
| j |
| CD |
| i |
| j |
| AD |
| AC |
| BD |
解答:
解:由题意得,
=6
+
=(6,1),
=x
+y
=(x,y),
=-2
-3
=(-2,-3),
=
+
+
=(6+x-2,1+y-3)=(4+x,y-2);
=
+
=(6+x,1+y);
=
+
=(x-2,y-3);
故由AD∥BC,AC⊥BD可得,
,
解得,x=2,y=-1或x=-6,y=3.
| AB |
| i |
| j |
| BC |
| i |
| j |
| CD |
| i |
| j |
| AD |
| i |
| AB |
| BC |
| CD |
| AC |
| i |
| AB |
| BC |
| BD |
| i |
| BC |
| CD |
故由AD∥BC,AC⊥BD可得,
|
解得,x=2,y=-1或x=-6,y=3.
点评:本题考查了平面向量的应用,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
把一根长度为5的铁丝截成任意长的3段,则能构成三角形的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
边长为2的正三角形ABC中,D,E,M分别是AB,AC,BC的中点,N为DE的中点,将△ADE沿DE折起至A′DE位置,使A′M=
,设MC的中点为Q,A′B的中点为P,则
①A′N⊥平面BCED
②NQ∥平面A′EC
③DE⊥平面A′MN
④平面PMN∥平面A′EC
以上结论正确的是( )
| ||
| 2 |
①A′N⊥平面BCED
②NQ∥平面A′EC
③DE⊥平面A′MN
④平面PMN∥平面A′EC
以上结论正确的是( )
| A、①②④ | B、②③④ |
| C、①②③ | D、①③④ |
(普通文科做)已知f(x)=x+
,则f(x)的单调递增区间为( )
| 4 |
| x |
| A、(-∞,-2] |
| B、[2,+∞) |
| C、(-∞,-2]与[2,+∞) |
| D、(-∞,-2]∪[2,+∞) |
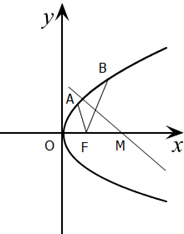 如图,已知抛物线C的顶点在原点,焦点点为圆x2+y2-2x=0的圆心,
如图,已知抛物线C的顶点在原点,焦点点为圆x2+y2-2x=0的圆心, 某海岛上有一座海拔1千米的山,山顶上有一观察站P(P在海平面上的射影点为A),测得一游艇在海岛南偏西30°,俯角为45°的B处,该游艇准备前往海岛正东方向,俯角为45°的旅游景点C处,如图所示.
某海岛上有一座海拔1千米的山,山顶上有一观察站P(P在海平面上的射影点为A),测得一游艇在海岛南偏西30°,俯角为45°的B处,该游艇准备前往海岛正东方向,俯角为45°的旅游景点C处,如图所示.