题目内容
某射手每次射击命中率均为p,若其连续射击2次均未命中目标的概率是
.
(1)求p的值;
(2)若该射手有4发子弹,最多进行4次独立的射击,若命中目标就停止,写出射击停止时射击次数ξ=3和ξ=4的概率.
| 1 |
| 9 |
(1)求p的值;
(2)若该射手有4发子弹,最多进行4次独立的射击,若命中目标就停止,写出射击停止时射击次数ξ=3和ξ=4的概率.
考点:相互独立事件的概率乘法公式
专题:概率与统计
分析:(1)由已知得(1-p)(1-p)=
,由此能求出p.
(2)ξ=3表示“前两次均没有命中目标,第三次才命中目标”,ξ=4表示“前三次均没有命中目标,第四次才命中目标或四次射击均没有命中目标”,由此能求出射击停止时射击次数ξ=3和ξ=4的概率.
| 1 |
| 9 |
(2)ξ=3表示“前两次均没有命中目标,第三次才命中目标”,ξ=4表示“前三次均没有命中目标,第四次才命中目标或四次射击均没有命中目标”,由此能求出射击停止时射击次数ξ=3和ξ=4的概率.
解答:
解:(1)由已知得(1-p)(1-p)=
,
解得p=
.
(2)ξ=3表示“前两次均没有命中目标,第三次才命中目标”,
∴P(ξ=3)=(1-
)(1-
)•
=
,
ξ=4表示“前三次均没有命中目标,第四次才命中目标或四次射击均没有命中目标”,
∴P(ξ=4)=(1-
)(1-
)(1-
)•
+(1-
)(1-
)(1-
)(1-
)=
.
| 1 |
| 9 |
解得p=
| 2 |
| 3 |
(2)ξ=3表示“前两次均没有命中目标,第三次才命中目标”,
∴P(ξ=3)=(1-
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 27 |
ξ=4表示“前三次均没有命中目标,第四次才命中目标或四次射击均没有命中目标”,
∴P(ξ=4)=(1-
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 27 |
点评:本题考查概率的求法,是中档题,解题时要认真审题,注意相互独立事件概率计算公式的合理运用.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
已知f(x)=
,则f[(
)
]的值是( )
|
| 1 |
| 2 |
| 3 |
| 2 |
| A、-1 | ||
| B、1 | ||
C、
| ||
D、-
|
已知p:方程
+
=1所表示的曲线为焦点在x轴上的椭圆,q:|t-a|<2(a∈N),若p是q的充分不必要条件,则a取值范围为( )
| x2 |
| 3-t |
| y2 |
| t+1 |
| A、(-∞,1] |
| B、[-1,1] |
| C、[0,+∞) |
| D、(0,1) |
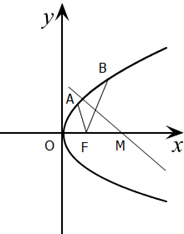 如图,已知抛物线C的顶点在原点,焦点点为圆x2+y2-2x=0的圆心,
如图,已知抛物线C的顶点在原点,焦点点为圆x2+y2-2x=0的圆心, 某海岛上有一座海拔1千米的山,山顶上有一观察站P(P在海平面上的射影点为A),测得一游艇在海岛南偏西30°,俯角为45°的B处,该游艇准备前往海岛正东方向,俯角为45°的旅游景点C处,如图所示.
某海岛上有一座海拔1千米的山,山顶上有一观察站P(P在海平面上的射影点为A),测得一游艇在海岛南偏西30°,俯角为45°的B处,该游艇准备前往海岛正东方向,俯角为45°的旅游景点C处,如图所示.