题目内容
全集U=R,集合A={x|3≤x<10},B={x|
(1)求A∩B,A∪B,(∁UA)∩(∁UB);
(2)若集合C={x|x>a},A⊆C,求a的取值范围(结果用区间表示).
|
(1)求A∩B,A∪B,(∁UA)∩(∁UB);
(2)若集合C={x|x>a},A⊆C,求a的取值范围(结果用区间表示).
考点:集合的包含关系判断及应用,交、并、补集的混合运算
专题:集合
分析:(1)解不等式组求出集合B,进而根据集合交集,并集,补集的定义及(CUA)∩(CUB)=CU(A∪B)得到答案;
(2)由集合C={x|x>a},A⊆C,可得a<3,用区间表示可得a的取值范围.
(2)由集合C={x|x>a},A⊆C,可得a<3,用区间表示可得a的取值范围.
解答:
解:(1)∵集合A={x|3≤x<10}=[3,10),
B={x|
=(2,7],
∴A∩B=[3,7]-----(3分);
A∪B=(2,10)-----(6分);
(CUA)∩(CUB)=CU(A∪B)=(-∞,2]∪[10,+∞)-------------(9分)
( 2)∵集合C={x|x>a},A⊆C,
∴<3,
∴a范围是(-∞,3)-------------(12分)
B={x|
|
∴A∩B=[3,7]-----(3分);
A∪B=(2,10)-----(6分);
(CUA)∩(CUB)=CU(A∪B)=(-∞,2]∪[10,+∞)-------------(9分)
( 2)∵集合C={x|x>a},A⊆C,
∴<3,
∴a范围是(-∞,3)-------------(12分)
点评:本题考查的知识点是集合的包含关系判断及应用,集合的交集,交集,补集运算,难度不大,属于基础题

练习册系列答案
相关题目
某商场有四类食品,其中粮食类、植物油类、动物食品类及果蔬类分别有40种、10种、20种、20种,现采用分层抽样的方法抽取样本进行食品安全检测,若抽取的动物类食品有6种,则样本容量为( )
| A、18 | B、22 | C、27 | D、36 |
已知f(x)=
,则f[(
)
]的值是( )
|
| 1 |
| 2 |
| 3 |
| 2 |
| A、-1 | ||
| B、1 | ||
C、
| ||
D、-
|
已知集合A={(x,y)|2x-y=0},集合B={(x,y)|x-y=3},则集合A∩B是( )
| A、{-6,-3} |
| B、{(-3,-6)} |
| C、{3,6} |
| D、(-3,-6) |

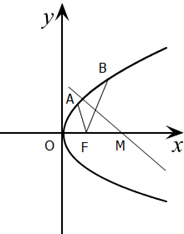 如图,已知抛物线C的顶点在原点,焦点点为圆x2+y2-2x=0的圆心,
如图,已知抛物线C的顶点在原点,焦点点为圆x2+y2-2x=0的圆心,