题目内容
12.已知F1,F2分别是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>0,b>0)的左、右焦点,P为椭圆上的一点,若∠F1PF2=90°,且△F1PF2的三边长成等差数列,则椭圆的离心率是( )| A. | $\frac{2}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{5}{7}$ |
分析 不妨设|PF2|>|PF1|,|PF1|,2a-|PF1|,2c成等差数列,从而得到|PF1|=$\frac{4a-2c}{3}$,|PF2|=$\frac{2a+2c}{3}$,由∠F1PF2=90°,得到|PF1|•|PF2|=$\frac{4a-2c}{3}•\frac{2a+2c}{3}$=2b2,由此能求出椭圆的离心率.
解答 解:∵F1,F2分别是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>0,b>0)的左、右焦点,P为椭圆上的一点,
∠F1PF2=90°,且△F1PF2的三边长成等差数列,
∴不妨设|PF2|>|PF1|,|PF1|,2a-|PF1|,2c成等差数列,
∴2(2a-|PF1|)=|PF1|+2c,
∴|PF1|=$\frac{4a-2c}{3}$,|PF2|=2a-$\frac{4a-2c}{3}$=$\frac{2a+2c}{3}$,
∵∠F1PF2=90°,∴|PF1|2+|PF2|2=4c2,
又|PF1|+|PF2|=2a,
∴|PF1|2+|PF2|2+2|PF1|•|PF2|=4a2,
∴|PF1|•|PF2|=$\frac{4a-2c}{3}•\frac{2a+2c}{3}$=2b2,
整理,得5a2-7c2-2ac=0,
∴7e2+2e-5=0,
解得e=$\frac{5}{7}$或e=-1(舍).
∴椭圆的离心率是$\frac{5}{7}$.
故选:D.
点评 本题考查椭圆离心率的求法,是中档题,解题时要认真审题,注意椭圆、等差数列、勾股定理、一元二次方程等知识点的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.三角形ABC中角A、B、C对边分别为a、b、c,且a=2,b=3,c=4.若长度为4的动线段PQ的中点恰为A点,则$\overrightarrow{BP}•\overrightarrow{CQ}$的最大值是( )
| A. | -$\frac{3}{2}$ | B. | $\frac{11}{2}$ | C. | $\frac{21}{2}$ | D. | $\frac{29}{2}$ |
3.复数z=i(-1+3i)在复平面上对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.设m为不小于2的正整数,对任意n∈Z,若n=qm+r(其中q,r∈Z,且0≤r<m),则记fm(n)=r,如f2(3)=1,f3(8)=2,下列关于该映射fm:Z→Z的命题中,不正确的是( )
| A. | 若a,b∈Z,则fm(a+b)=fm(a)+fm(b) | |
| B. | 若a,b,k∈Z,且fm(a)=fm(b),则fm(ka)=fm(kb) | |
| C. | 若a,b,c,d∈Z,且fm(a)=fm(b),fm(c)=fm(d),则fm(a+c)=fm(b+d) | |
| D. | 若a,b,c,d∈Z,且fm(a)=fm(b),fm(c)=fm(d),则fm(ac)=fm(bd) |
17.已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的最小正周期为4π,且对?x∈R,有f(x)≤f($\frac{π}{3}$)成立,则f(x)的一个对称中心坐标是( )
| A. | (-$\frac{2π}{3}$,0) | B. | (-$\frac{π}{3}$,0) | C. | ($\frac{2π}{3}$,0) | D. | ($\frac{5π}{3}$,0) |
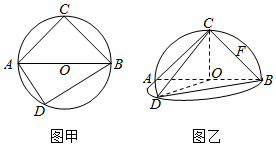 如图甲:⊙O的直径AB=2,圆上两点C,D在直径AB的两侧,使∠CAB=$\frac{π}{4}$,∠DAB=$\frac{π}{3}$,沿直径AB折起,使两个半圆所在的平面互相垂直(如图乙),F为BC的中点,根据图乙解答下列各题:
如图甲:⊙O的直径AB=2,圆上两点C,D在直径AB的两侧,使∠CAB=$\frac{π}{4}$,∠DAB=$\frac{π}{3}$,沿直径AB折起,使两个半圆所在的平面互相垂直(如图乙),F为BC的中点,根据图乙解答下列各题: 已知正方体ABCD-A1B1C1D1,点E为棱AA1的中点,则异面直线B1D1与DE所成角的大小是arccos$\frac{\sqrt{10}}{5}$(结果用反三角函数值表示)
已知正方体ABCD-A1B1C1D1,点E为棱AA1的中点,则异面直线B1D1与DE所成角的大小是arccos$\frac{\sqrt{10}}{5}$(结果用反三角函数值表示)