题目内容
圆柱的轴截面ABCD是边长为2的正方形，M为正方形ABCD的对角线的交点，动点P在圆柱下底面内（包括圆周），若直线AM与直线MP所成的角为45°，则点P形成的轨迹为（ ）
| A、椭圆的一部分 |
| B、抛物线的一部分 |
| C、双曲线的一部分 |
| D、圆的一部分 |
考点：旋转体（圆柱、圆锥、圆台）
专题：圆锥曲线的定义、性质与方程
分析：根据已知，可得直线AM与圆柱底面的夹角为45°，此时点P形成的轨迹相当于底面截取以AM为轴，轴截面顶角为90°的圆锥所得曲线的一部分，结合圆锥曲线的定义，可得答案．
解答：
解：∵直线AM与直线MP所成的角为45°，
故点P形成的轨迹相当于底面截取以AM为轴，轴截面顶角为90°的圆锥所得曲线的一部分，
∵圆柱的轴截面ABCD是边长为2的正方形，M为正方形ABCD的对角线的交点，
故底面与圆锥轴夹角为45°，
故点P形成的轨迹为抛物线的一部分，
故选：B
故点P形成的轨迹相当于底面截取以AM为轴，轴截面顶角为90°的圆锥所得曲线的一部分，
∵圆柱的轴截面ABCD是边长为2的正方形，M为正方形ABCD的对角线的交点，
故底面与圆锥轴夹角为45°，
故点P形成的轨迹为抛物线的一部分，
故选：B
点评：本题考查的知识点是圆锥曲线的定义，本题转化困难，不容易理解，属于难题．
练习册系列答案
相关题目
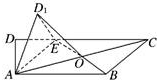如图，在梯形ABCD中，AB∥CD，∠ADC=90°，AB=2，DC=3，AD=1．E是DC上一点，且DE=1，连接AE，将△DAE沿AE折起到△D1AE的位置，使得∠D1AB=30°，设AC与BE的交点为O．
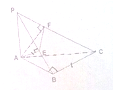如图，P为△ABC所在平面外一点，PA⊥平面ABC，∠ABC=90°，AE⊥PB于E，AF⊥PC于F．求证：