题目内容
若
、
是一组基底,且
=
+
,
=
-2
,
=2
+3
,则用向量
、
来表示
的式子为 .
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
| c |
| e1 |
| e2 |
| b |
| c |
| a |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:设
=λ
+μ
,所以便得到
=
+
=(λ+2μ)
+(3μ-2λ)
,
,
是一组基底,所以根据平面向量基本定理得到
,解出λ,μ即可用
,
表示
了.
| a |
| b |
| c |
| a |
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
|
| b |
| c |
| a |
解答:
解:设
=λ
+μ
;
∴
+
=λ(
-2
)+μ(2
+3
)=(λ+2μ)
+(3μ-2λ)
;
∵
,
是一组基底;
∴
;
解得λ=
,μ=
;
∴
=
+
.
故答案为:
=
+
.
| a |
| b |
| c |
∴
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
∵
| e1 |
| e2 |
∴
|
解得λ=
| 1 |
| 7 |
| 3 |
| 7 |
∴
| a |
| 1 |
| 7 |
| b |
| 3 |
| 7 |
| c |
故答案为:
| a |
| 1 |
| 7 |
| b |
| 3 |
| 7 |
| c |
点评:考查向量的数乘运算,加法运算,以及基底的概念,平面向量基本定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
圆柱的轴截面ABCD是边长为2的正方形,M为正方形ABCD的对角线的交点,动点P在圆柱下底面内(包括圆周),若直线AM与直线MP所成的角为45°,则点P形成的轨迹为( )
| A、椭圆的一部分 |
| B、抛物线的一部分 |
| C、双曲线的一部分 |
| D、圆的一部分 |
若双曲线x2-y2=a2(a>0)的左、右顶点分别为A、B,点P是第一象限内双曲线上的点.记∠PAB=α,且∠PBA=β,则( )
A、α+β=
| ||
B、β-α=
| ||
| C、β=2α | ||
| D、β=3α |
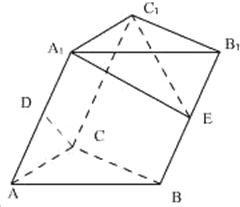 在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥面ABC,AA1=
在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥面ABC,AA1=