题目内容
已知,⊙O的圆心在直线x+y-1=0上,且与y轴、x轴相切,求该圆的标准方程.
考点:圆的标准方程
专题:直线与圆
分析:设出圆心坐标,利用圆和坐标轴相切建立条件关系即可得到结论.
解答:
解:∵圆心在直线x+y-1=0上,
∴设圆心坐标为(a,1-a),
∵圆与y轴、x轴相切,
∴|a|=|1-a|=r,
解得a=
,即圆心为(
,
),半径r=
,
则圆的标准方程为(x-
)2+(y-
)2=
.
∴设圆心坐标为(a,1-a),
∵圆与y轴、x轴相切,
∴|a|=|1-a|=r,
解得a=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
则圆的标准方程为(x-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
点评:本题主要考查圆的标准方程的求解,根据条件利用待定系数法是解决本题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
圆柱的轴截面ABCD是边长为2的正方形,M为正方形ABCD的对角线的交点,动点P在圆柱下底面内(包括圆周),若直线AM与直线MP所成的角为45°,则点P形成的轨迹为( )
| A、椭圆的一部分 |
| B、抛物线的一部分 |
| C、双曲线的一部分 |
| D、圆的一部分 |
函数f(x)=
有且只有一个零点的充分不必要条件是( )
|
| A、a<0 | ||
B、0<a<
| ||
C、
| ||
| D、a≤0或a>1 |
 如图,在△ABC中,
如图,在△ABC中,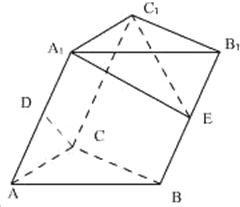 在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥面ABC,AA1=
在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥面ABC,AA1=