题目内容
(1)已知圆的方程是(x+4)2+(y-2)2=9,求经过点P(-1,5)的切线方程.
(2)点P是椭圆
+
=1上的动点,A(1,0),求PA的最大、小值.
(2)点P是椭圆
| x2 |
| 16 |
| y2 |
| 12 |
考点:两点间的距离公式,圆的切线方程
专题:直线与圆,圆锥曲线中的最值与范围问题
分析:(1)利用直线与圆相切的充要条件即可得出.
(2)利用两点间的距离公式和二次函数的单调性即可得出.
(2)利用两点间的距离公式和二次函数的单调性即可得出.
解答:
解:(1)由(x+4)2+(y-2)2=9可得圆心(-4,2),半径r=3.
可知:当直线x=-1时与此圆相切,是圆的一条切线.
当经过点P(-1,5)的切线的斜率存在时,设切线方程为y-5=k(x+1),
由直线与圆相切可得
=3,解得k=0.
∴切线的方程为y=5.
综上可知:经过点P(-1,5)的切线方程为y=5,或x=-1.
(2)设点P(x,y).则-4≤x≤4.
由
+
=1,得y2=12-
x2,
∴|PA|=
=
=
=
.
∵-4≤x≤4,∴函数
(x-4)2+9单调递减..
故当且仅当x=4时,|PA|取得最小值3;x=-4时,|PA|取得最大值5.
可知:当直线x=-1时与此圆相切,是圆的一条切线.
当经过点P(-1,5)的切线的斜率存在时,设切线方程为y-5=k(x+1),
由直线与圆相切可得
| |-4k-2+5+k| | ||
|
∴切线的方程为y=5.
综上可知:经过点P(-1,5)的切线方程为y=5,或x=-1.
(2)设点P(x,y).则-4≤x≤4.
由
| x2 |
| 16 |
| y2 |
| 12 |
| 3 |
| 4 |
∴|PA|=
| (x-1)2+y2 |
(x-1)2+12-
|
|
|
∵-4≤x≤4,∴函数
| 1 |
| 4 |
故当且仅当x=4时,|PA|取得最小值3;x=-4时,|PA|取得最大值5.
点评:熟练掌握直线与圆相切的充要条件、两点间的距离公式和二次函数的单调性是解题的关键.

练习册系列答案
相关题目
设全集I=R,T={x|x2<x},M={x|x∉T},则M等于( )
| A、{x|x≥1} |
| B、{x|x>1} |
| C、{x|-1≤x≤0} |
| D、{x|x≥1或x≤0} |
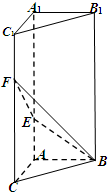 如图,在直三棱柱ABC-A1B1C1中,
如图,在直三棱柱ABC-A1B1C1中, 如图,AB为半圆的直径,P为半圆上一点,|AB|=10,∠PAB=a,且sina=
如图,AB为半圆的直径,P为半圆上一点,|AB|=10,∠PAB=a,且sina=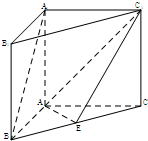 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.