题目内容
6．函数y=ax2-2x的图象上有且仅有两个点到直线y=x的距离等于$\sqrt{2}$，则实数a的取值集合是{a|a＜-$\frac{9}{8}$或a=0或a$＞\frac{9}{8}$}．分析 对a进行分类讨论，得出y=ax2-2x与y=x±2的位置关系，根据交点个数判断a的范围．
解答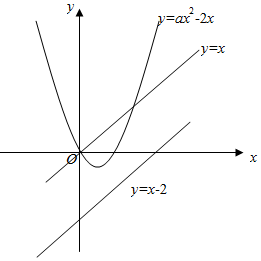 
解：（1）若a=0，则y=2x与y=x为相交直线，
显然y=2x上存在两点到y=x的距离等于$\sqrt{2}$，符合题意；
（2）若a＞0，则y=ax2-2x与直线y=x相交，
∴y=ax2-2x在直线y=x上方的图象必有2点到直线y=x的距离等于$\sqrt{2}$，
又直线y=x与y=x-2的距离为$\sqrt{2}$，
∴抛物线y=ax2-2x与直线y=x-2不相交，
联立方程组$\left\{\begin{array}{l}{y=a{x}^{2}-2x}\\{y=x-2}\end{array}\right.$，消元得ax2-3x+2=0，
∴△=9-8a＜0，解得a$＞\frac{9}{8}$．
（3）若a＜0，同理可得a＜-$\frac{9}{8}$．
故答案为：{a|a＜-$\frac{9}{8}$或a=0或a$＞\frac{9}{8}$}．
点评 本题考查了二次函数的性质，直线与曲线的位置关系，属于中档题．
练习册系列答案
相关题目
函数f（x）=Asin（ωx+φ）（A，ω＞0，|φ|＜$\frac{π}{2}$）的图象如图所示，则tanφ=$\sqrt{3}$．