Question

5．甲和乙两人约定在某天早上6：30到7：30之间在校门口见面，假设每人都是随机的在这个小时内的任意时刻到达，且只等15分钟．则他们能碰面的概率是$\frac{7}{16}$．

Answer 1

分析 由题意知本题是一个几何概型，试验包含的所有事件是Ω={（x，y）|6.5≤x≤7.5，6.5≤y≤7.5}，做出事件对应的集合表示的面积，写出满足条件的事件是A={（x，y）|6.5≤x≤7.5，6.5≤y≤7.5，|x-y|≤$\frac{1}{4}$}，算出事件对应的集合表示的面积，根据几何概型概率公式得到结果．

解答 解：由题意知本题是一个几何概型，设事件A为“两人能会面”，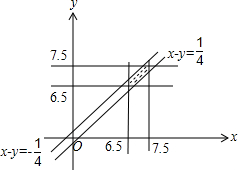
试验包含的所有事件是Ω={（x，y）|6.5≤x≤7.5，6.5≤y≤7.5}，并且事件对应的集合表示的面积是s=1，
满足条件的事件是A={（x，y）|6.5≤x≤7.5，6.5≤y≤7.5，|x-y|≤$\frac{1}{4}$}，
∴事件对应的集合表示的面积是1-2×$\frac{1}{2}×\frac{3}{4}×\frac{3}{4}$=$\frac{7}{16}$．
根据几何概型概率公式得到P=$\frac{7}{16}$．
故答案为：$\frac{7}{16}$．

点评 本题是一个几何概型，对于这样的问题，一般要通过把试验发生包含的事件同集合结合起来，根据集合对应的图形做出面积，用面积的比值得到结果，是基础题．