题目内容
19.设M=2a2-4a,N=a2-2a-3,则有( )| A. | M<N | B. | M≤N | C. | M>N | D. | M≥N |
分析 作差后,利用配方法判断差的符号,即可比较出大小关系.
解答 解:∵M=2a2-4a,N=a2-2a-3,、
∴M-N=a2-2a+3=(a+1)2+2>0,
∴M>N,
故选:C
点评 本题考查了作差法比较数的大小关系、配方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
4.已知y=f(x)是定义在R上的增函数且为奇函数,若对任意的x,y∈R,不等式f(x2-6x+21)+f(y2-8y)<0恒成立,则当x>3时,x2+y2的取值范围是( )
| A. | (3,7) | B. | (9,25) | C. | (13,49) | D. | (9,49) |
11.函数$y={(\frac{1}{3})^{|x|}}-1$的值域是( )
| A. | [1,+∞) | B. | [0,+∞) | C. | (-∞,0] | D. | (-1,0] |
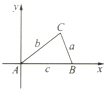 补全用解析法证明余弦定理的过程.
补全用解析法证明余弦定理的过程.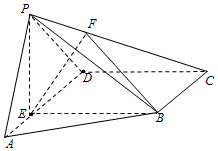 如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD.AD∥BC,AD⊥CD,BC=ED=2AE=2,EB=3,F为PC上一点,且CF=2FP.
如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD.AD∥BC,AD⊥CD,BC=ED=2AE=2,EB=3,F为PC上一点,且CF=2FP.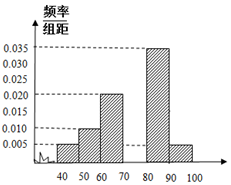 为了估计某校的一次数学考试情况,现从该校参加考试的600名学生中随机抽出60名学生,其成绩(百分制)均在[40,100)上,将这些成绩分成六段[40,50),[50,60)…[90,100),后得到如图所示部分频率分布直方图.
为了估计某校的一次数学考试情况,现从该校参加考试的600名学生中随机抽出60名学生,其成绩(百分制)均在[40,100)上,将这些成绩分成六段[40,50),[50,60)…[90,100),后得到如图所示部分频率分布直方图.