题目内容
1. 已知A,B是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1左、右顶点,过椭圆中心0作弦MN交椭圆于M,N两点,且$\overrightarrow{AN}$$•\overrightarrow{MN}$=0,|$\overrightarrow{MN}$|=2|$\overrightarrow{AN}$|.
已知A,B是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1左、右顶点,过椭圆中心0作弦MN交椭圆于M,N两点,且$\overrightarrow{AN}$$•\overrightarrow{MN}$=0,|$\overrightarrow{MN}$|=2|$\overrightarrow{AN}$|.(1)求该椭圆的离心率;
(2)如图所示,过顶点B作平行于y轴的直线BC,连接OC,过点A作弦AD∥OC交椭圆于D点,过点D作DE⊥AB于点E,连接AC交DE于P点,求证:|$\overrightarrow{DE}$|=2|$\overrightarrow{DP}$|.
分析 (1)由题意知AN⊥NO,且|AN|=|ON|,从而可得点N(-$\frac{a}{2}$,-$\frac{a}{2}$),从而可得a2=3b2,从而求椭圆的离心率;
(2)由题意作图象,设直线AD与直线BC相交于点M,从而利用平行及相似证明即可.
解答 解:(1)∵$\overrightarrow{AN}$$•\overrightarrow{MN}$=0,
∴AN⊥NO,
又∵|$\overrightarrow{MN}$|=2|$\overrightarrow{AN}$|,
∴|AN|=|ON|,又∵|OA|=a,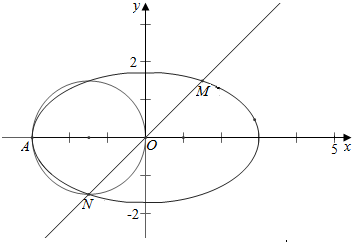
∴点N(-$\frac{a}{2}$,-$\frac{a}{2}$),
故$\frac{(-\frac{a}{2})^{2}}{{a}^{2}}$+$\frac{(-\frac{a}{2})^{2}}{{b}^{2}}$=1,
解得,a2=3b2,
故e=$\frac{c}{a}$=$\frac{\sqrt{2}b}{\sqrt{3}b}$=$\frac{\sqrt{6}}{3}$,
故该椭圆的离心率为$\frac{\sqrt{6}}{3}$;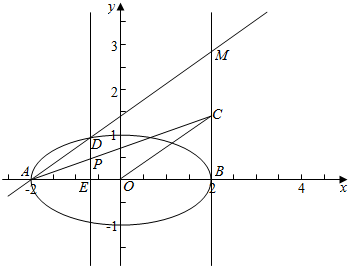
(2)证明:由题意作图象如右图,
设直线AD与直线BC相交于点M,
∵O是AB的中点,
又∵AD∥OC,
∴OC是△ABM的中位线,
∴BC=BM,
∵DE∥BM,
∴$\frac{DP}{MC}$=$\frac{AP}{AC}$=$\frac{PE}{BC}$,
∴DP=PE,
∴|$\overrightarrow{DE}$|=2|$\overrightarrow{DP}$|.
点评 本题考查了数形结合的思想应用,同时考查了圆锥曲线的定义及性质的应用,同时考查了圆锥曲线与直线的位置关系的应用.

练习册系列答案
相关题目
12.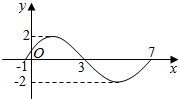 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的一个周期的图象,如图所示,则f(x)的解析式为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的一个周期的图象,如图所示,则f(x)的解析式为( )
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的一个周期的图象,如图所示,则f(x)的解析式为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的一个周期的图象,如图所示,则f(x)的解析式为( )| A. | 2sin($\frac{x}{4}$-$\frac{π}{4}$) | B. | 2sin($\frac{x}{4}$+$\frac{π}{4}$) | C. | 2sin($\frac{πx}{4}$-$\frac{π}{4}$) | D. | 2sin($\frac{πx}{4}$+$\frac{π}{4}$) |
9.某几何体的三视图如图所示,则此几何体的体积等于( )
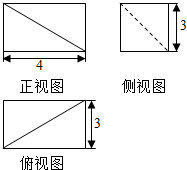

| A. | 45 | B. | 36 | C. | 30 | D. | 6 |
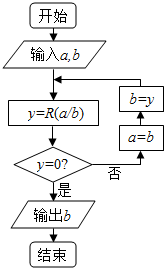 “辗转相除法”的算法思路如右图所示.记R(a\b)为a除以b所得的余数(a,b∈N*),执行程序框图,若输入a,b分别为243,45,则输出b的值为( )
“辗转相除法”的算法思路如右图所示.记R(a\b)为a除以b所得的余数(a,b∈N*),执行程序框图,若输入a,b分别为243,45,则输出b的值为( )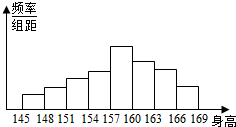 为了了解中学生的身高情况,对某中学同龄的若干女生身高进行测量,将所得数据整理后,画出频率分布直方图如图所示,已知图中从左到右五个小组的频率分别为0.017,0.050,0.100,0.133,0.300,第三个小组的频数为6.
为了了解中学生的身高情况,对某中学同龄的若干女生身高进行测量,将所得数据整理后,画出频率分布直方图如图所示,已知图中从左到右五个小组的频率分别为0.017,0.050,0.100,0.133,0.300,第三个小组的频数为6.