题目内容
11.在空间直角坐标系O-xyz中,经过点P(2,1,1)且与直线$\left\{{\begin{array}{l}{x-3y+z+1=0}\\{3x-2y-2z+1=0}\end{array}}\right.$垂直的平面方程为8x+5y+7z-28=0.分析 设两条直线的方向向量分别为(1,-3,1)(3,-2,-2),设平面的法向量为(x,y,z),则由$\left\{\begin{array}{l}{x-3y+z=0}\\{3x-2y-2z=0}\end{array}\right.$得到一法向量为(1,$\frac{5}{8}$,$\frac{7}{8}$),得到所求平面方程.
解答 解:设两条直线的方向向量分别为(1,-3,1)(3,-2,-2),
设平面的法向量为(x,y,z),则由$\left\{\begin{array}{l}{x-3y+z=0}\\{3x-2y-2z=0}\end{array}\right.$得到一法向量为(1,$\frac{5}{8}$,$\frac{7}{8}$),
所以与直线$\left\{{\begin{array}{l}{x-3y+z+1=0}\\{3x-2y-2z+1=0}\end{array}}\right.$垂直的平面方程为(x-2)×1+$\frac{5}{8}$(y-1)+$\frac{7}{8}$(z-1)=0,
整理得8x+5y+7z-28=0;
故答案为:8x+5y+7z-28=0
点评 本题考查了由向量的坐标求平面方程;关键是求出与两条直线垂直的向量坐标.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
19.使函数f(x)=$\root{3}{{x}^{2}(1-{x}^{2})}$满足罗尔定理条件的区间是( )
| A. | [0,1] | B. | [-1,1] | C. | [-2,2] | D. | [-$\frac{3}{5}$,$\frac{4}{5}$] |
19.已知直线l与双曲线$\frac{x^2}{4}-{y^2}=1$相切于点P,l与双曲线两条渐进线交于M,N两点,则$\overrightarrow{OM}•\overrightarrow{ON}$的值为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 与P的位置有关 |
6.已知函数$f(x)=\left\{\begin{array}{l}({a-1})x+4-2a,x<1\\ 1+{log_2}x,x≥1\end{array}\right.$,若f(x)的值域为R,则实数a的取值范围是( )
| A. | (1,2] | B. | (-∞,2] | C. | (0,2] | D. | [2,+∞) |
1.已知函数f(x)=cos(2x+φ),且${∫}_{0}^{\frac{2}{3}π}$f(x)dx=0,则下列说法正确的是( )
| A. | f(x)的一条对称轴为x=$\frac{5π}{12}$ | |
| B. | 存在φ使得f(x)在区间[-$\frac{π}{6}$,$\frac{π}{3}$]上单调递减 | |
| C. | f(x)的一个对称中心为($\frac{5π}{12}$,0) | |
| D. | 存在φ使得f(x)在区间[$\frac{π}{12}$,$\frac{7π}{12}$]上单调递增 |
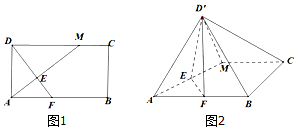 如图,在矩形ABCD中,AB=2BC,点M在边CD上,点F在边AB上,且DF⊥AM,垂足为E,若将△ADM沿AM折起,使点D位于D′位置,连接D′B,D′C,得四棱锥D′-ABCM.
如图,在矩形ABCD中,AB=2BC,点M在边CD上,点F在边AB上,且DF⊥AM,垂足为E,若将△ADM沿AM折起,使点D位于D′位置,连接D′B,D′C,得四棱锥D′-ABCM.