题目内容
解不等式：0＜|x-4|≤3．
考点：绝对值不等式的解法
专题：不等式的解法及应用
分析：由题意可得可得0＜x-4≤3 ①，或-3≤x-4＜0 ②，分别求得①和②的解集，再取并集，即得所求．
解答：
解：由0＜|x-4|≤3，可得0＜x-4≤3 ①或-3≤x-4＜0 ②，
由①求得4＜x≤7，解②求得1≤x＜4，故不等式的解集为{x|1≤x＜4，或4＜x≤7}．
由①求得4＜x≤7，解②求得1≤x＜4，故不等式的解集为{x|1≤x＜4，或4＜x≤7}．
点评：本题主要考查绝对值不等式的解法，体现了等价转化、分类讨论的数学思想，属于基础题．
练习册系列答案
相关题目
下列命题错误的是（ ）
A、若
| ||||||||
B、若
| ||||||||
C、当m∈R时，恒有m（
| ||||||||
D、|
|
己知定义在实数集R上的函数f（x）满足：
①f（2-x）=f（x）；②f（x+2）=f（x-2）；③当x1，x2∈[1，3]时，
＞0，
则f（2014）、f（2015）、f（2016）满足（ ）
①f（2-x）=f（x）；②f（x+2）=f（x-2）；③当x1，x2∈[1，3]时，
| f(x1)-f(x2) |
| x1-x2 |
则f（2014）、f（2015）、f（2016）满足（ ）
| A、f（2014）＞f（2015）＞f（2016） |
| B、f（2016）＞f（2015）＞f（2014） |
| C、f（2016）=f（2014）＞f（2015） |
| D、f（2016）=f（2014）＜f（2015） |
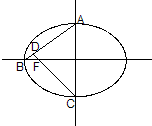已知如图，椭圆的离心率为| 1 |
| 2 |
A、-3
| ||
B、3-
| ||
C、3
| ||
D、3+
|