题目内容
4.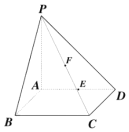 如图:在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是正方形,PA=AD=2.
如图:在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是正方形,PA=AD=2.(1)求异面直线PC与AB所成角的大小(结果用反三角函数值表示);
(2)求点E、F分别是棱AD和PC的中点,求证:EF⊥平面PBC.
分析 (1)以点A为原点,以AB方向为x轴正方向,AD方向为y轴正方向,建立空间直角坐标系,利用向量法能求出异面直线PC与AB所成角的大小.
(2)求出$\overrightarrow{EF}=(1,0,1)$,$\overrightarrow{BC}=(0,2,0)$,$\overrightarrow{PC}=(2,2,-2)$,利用向量法能证明EF⊥平面PBC.
解答 解:(1)以点A为原点,以AB方向为x轴正方向,AD方向为y轴正方向,建立空间直角坐标系,
则P(0,0,2),A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0)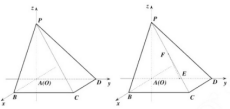
所以,$\overrightarrow{PC}=(2,2,-2)$,$\overrightarrow{AB}=(2,0,0)$,
设$\overrightarrow{PC}$,$\overrightarrow{AB}$的夹角为α,
则$cosα=\frac{{\overrightarrow{PC}•\overrightarrow{AB}}}{{|\overrightarrow{PC}|•|\overrightarrow{AB}|}}=\frac{4}{{2\sqrt{3}•2}}=\frac{{\sqrt{3}}}{3}$,
所以$\overrightarrow{PC}$,$\overrightarrow{AB}$的夹角为$arccos\frac{{\sqrt{3}}}{3}$,
即异面直线PC与AB所成角的大小为$arccos\frac{{\sqrt{3}}}{3}$.
证明:(2)因为点E、F分别是棱AD和PC的中点,
可得E(0,1,0),F(1,1,1),所以$\overrightarrow{EF}=(1,0,1)$,
又$\overrightarrow{BC}=(0,2,0)$,$\overrightarrow{PC}=(2,2,-2)$,
计算可得$\overrightarrow{EF}•\overrightarrow{PC}=0$,$\overrightarrow{EF}•\overrightarrow{BC}=0$,
所以,EF⊥PC,EF⊥BC,又PC∩BC=C,
所以EF⊥平面PBC.
点评 本题考查直线与直线、直线与平面、平面与平面的位置关系等基础知识,考查推理论证能力、运算求解能力、空间思维能力,考查化归转化思想、数形结合思想,是中档题.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案| A. | 奇函数,且在(0,e)上是增函数 | B. | 奇函数,且在(0,e)上是减函数 | ||
| C. | 偶函数,且在(0,e)上是增函数 | D. | 偶函数,且在(0,e)上是减函数 |
| A. | $2\sqrt{5}-1$ | B. | $2\sqrt{5}$ | C. | 3 | D. | 4 |
| A. | 向右平移$\frac{π}{2}$个单位 | B. | 向右平移$\frac{π}{4}$个单位 | ||
| C. | 向左平移$\frac{π}{2}$个单位 | D. | 向左平移$\frac{π}{4}$个单位 |
| A. | (-∞,-2016) | B. | (-2018,-2016) | ||
| C. | (-2018,+∞) | D. | (-∞,-2018)∪(-2016,+∞) |
| A. | 12 | B. | 24 | C. | 36 | D. | 48 |
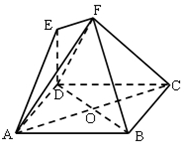 如图,多面体EF-ABCD中,四边形ABCD是菱形,AB=4,∠BAD=60°,AC,BD相交于O,EF∥AC,点E在平面ABCD上的射影恰好是线段AO的中点.
如图,多面体EF-ABCD中,四边形ABCD是菱形,AB=4,∠BAD=60°,AC,BD相交于O,EF∥AC,点E在平面ABCD上的射影恰好是线段AO的中点.