题目内容
函数f(x)=
的最大值与最小值的和为（ ）
2x2+
| ||||
| 2x2+cosx |
| A、π | B、2 | C、1 | D、0 |
考点：三角函数的最值
专题：函数的性质及应用
分析：先化简函数，然后判断函数g（x）=
为奇函数，利用奇函数的最大值和最小值之为0，然后利用图象平移得到函数f（x）=1+
的最大值与最小值的和．
| sinx+x |
| 2x2+cosx |
| sinx+x |
| 2x2+cosx |
解答：
解：f(x)=
=1+
，
设g（x）=
，则g（x）为奇函数，
∴函数g（x）的最大值与最小值互为相反数，即g（x）的最大值与最小值之和为0，
将函数g（x）向上平移一个单位得到函数f（x）=1+
的图象，
∴此时函数f（x）=1+
的最大值与最小值的和为2．
故选：B．
2x2+
| ||||
| 2x2+cosx |
| sinx+x |
| 2x2+cosx |
设g（x）=
| sinx+x |
| 2x2+cosx |
∴函数g（x）的最大值与最小值互为相反数，即g（x）的最大值与最小值之和为0，
将函数g（x）向上平移一个单位得到函数f（x）=1+
| sinx+x |
| 2x2+cosx |
∴此时函数f（x）=1+
| sinx+x |
| 2x2+cosx |
故选：B．
点评：本题考查了函数奇偶性的应用以及函数图象之间的关系，奇函数的最大值和最小值互为相反数是解决本题的关键．属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
下列函数中是偶函数的是（ ）
| A、y=x-2 | ||
| B、y=|3-x| | ||
| C、y=x2+2 x∈（-3，3] | ||
D、y=-
|
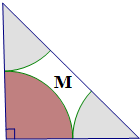如图，一个等腰直角三角形的直角边长为2，分别以三个顶点为圆心，1为半径在三角形内作圆弧，三段圆弧与斜边围成区域M（图中白色部分）．若在此三角形内随机取一点P，则点P落在区域M内的概率为（ ）
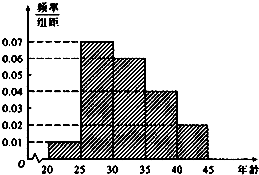某市为增强市民的环境保护意识，面向全市征召义务宣传志愿者．现从符合条件的志愿者中随机抽取100名按年龄分组：第1组[20，25），第2组[25，30），第3组[30，35），第4组[35，40），第5组[40，45]，得到的频率分布直方图如图所示．