题目内容
7.已知实数m,n满足logam>logan(a>1),则下列关系式不恒成立的是( )| A. | |m|>|n| | B. | ($\frac{1}{2}$)m<($\frac{1}{2}$)n | C. | sinm>sinn | D. | m${\;}^{\frac{1}{2}}$>n${\;}^{\frac{1}{2}}$ |
分析 由对数函数的单调性质得到m>n>0,由正弦函数的周期得:sinm>simn不一定成立.
解答 解:∵实数m,n满足logam>logan(a>1),
∴m>n>0,
∴|m|>|n|,($\frac{1}{2}$)m<($\frac{1}{2}$)n,m${\;}^{\frac{1}{2}}$>n${\;}^{\frac{1}{2}}$,
由正弦函数的周期得:sinm>simn不一定成立.
故选:C.
点评 本题考查命题真假的判断,是基础题,解题时要认真审题,注意对数函数、指数函数、三角函数的性质的合理运用.

练习册系列答案
相关题目
12.用随机事件发生的频率去估算这个事件发生的概率.下列结论正确的是( )
| A. | 事件A发生的概率P(A)是0<P(A)<1 | |
| B. | 事件A发生的概率P(A)=0.999,则事件A是必然事件 | |
| C. | 用某种药物对患有胃溃疡的500名病人治疗,结果有380人有明显的疗效,现有胃溃疡的病人服用此药,则估计有明显疗效的可能性为76% | |
| D. | 某奖券中奖率为0.5,则某人购买此券10张,一定有5张中奖 |
19.已知p:3+3=5,q:5>2,则下列判断错误的是( )
| A. | “p或q”为真,“非q”为假 | B. | “p且q”为假,“非p”为假 | ||
| C. | “p且q”为假,“非p”为真 | D. | “p且q”为假,“p或q”为真 |
17.执行如图所示的程序框图,则输出的n的值是( )


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
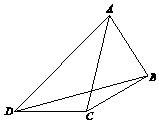 在如图所示的平面图形中,已知CD=$\sqrt{2}$,∠BCA=45°,∠ACD=105°,∠CDB=15°,∠BDA=30°.
在如图所示的平面图形中,已知CD=$\sqrt{2}$,∠BCA=45°,∠ACD=105°,∠CDB=15°,∠BDA=30°.