题目内容
7.已知圆C:(x-3)2+(y+1)2=4,过P(1,5)的直线l与圆C相切,则直线l的方程为x=1或4x+3y-19=0.分析 设出切线方程,求出圆的圆心与半径,利用圆心到直线的距离等于半径,求出k,写出切线方程即可.
解答 解:设切线方程为y-5=k(x-1),即kx-y-k+5=0,
∵圆心(3,-1)到切线l的距离等于半径2,
∴$\frac{|2k+6|}{\sqrt{{k}^{2}+1}}$=2,解得k=-$\frac{4}{3}$,
∴切线方程为4x+3y-19=0,
当过点M的直线的斜率不存在时,其方程为x=1,圆心(3,-1)到此直线的距离等于半径2,
故直线x=1也适合题意.
所以,所求的直线l的方程是x=1或4x+3y-19=0.
故答案为x=1或4x+3y-19=0.
点评 本题考查圆的切线方程的求法,注意直线的斜率存在与不存在情况,是本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.已知集合A={x||x-1|<1},B={x|1-$\frac{1}{x}$≥0},则A∩B=( )
| A. | {x|1≤x<2} | B. | {x|0<x<2} | C. | {x|0<x≤1} | D. | {x|0<x<1} |
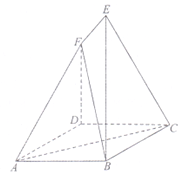 如图,ABCD是边长为a的菱形,∠BAD=60°,EB⊥平面ABCD,FD⊥平面ABCD,EB=2FD=$\sqrt{3}$a
如图,ABCD是边长为a的菱形,∠BAD=60°,EB⊥平面ABCD,FD⊥平面ABCD,EB=2FD=$\sqrt{3}$a