题目内容
13.若函数$y=\frac{ax+2}{x+2}$在区间(-2,+∞)上是增函数,则a的取值范围为(1,+∞).分析 令导函数y′>0恒成立即可得出a的范围.
解答 解:y′=$\frac{a(x+2)-(ax+2)}{(x+2)^{2}}$=$\frac{2a-2}{(x+2)^{2}}$,
∵函数$y=\frac{ax+2}{x+2}$在区间(-2,+∞)上是增函数,
∴$\frac{2a-2}{(x+2)^{2}}$>0在(-2,+∞)上恒成立,
∴2a-2>0,即a>1,
故答案为(1,+∞).
点评 本题考查了函数的单调性判断,属于中档题.

练习册系列答案
相关题目
1.已知函数y=2sin(ωx+φ)(ω>0,0<φ<π)的部分图象如图所示,则φ=( )
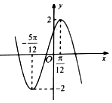

| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
5.平面直角坐标系中,在直线x=1,y=1与坐标轴围成的正方形内任取一点,则此点落在曲线y=x2下方区域的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |