题目内容
12.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-y2=1的一条渐近线与直线x+y+1=0垂直,则该双曲线的焦距为( )| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
分析 求得双曲线的渐近线方程,由两直线垂直的条件:斜率之积为-1,即可得到a的值,进而得到双曲线的a,b,c,以及焦距.
解答 解:双曲线$\frac{{x}^{2}}{{a}^{2}}$-y2=1的渐近线方程为y=±$\frac{x}{a}$,
渐近线与直线x+y+1=0垂直,可得渐近线的斜率为1,
可得a=±1,则双曲线的方程为x2-y2=1,
则a=b=1,c=$\sqrt{2}$,焦距为2$\sqrt{2}$.
故选:C.
点评 本题考查双曲线的方程和性质,主要是渐近线方程的运用,考查两直线垂直的条件:斜率之积为-1,考查运算能力,属于基础题.

练习册系列答案
相关题目
1.已知函数y=2sin(ωx+φ)(ω>0,0<φ<π)的部分图象如图所示,则φ=( )
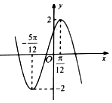

| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
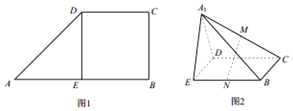 如图1.在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2CD,DE⊥AB,沿DE将△AEDD折起到△A1ED的位置,连结A1B,A1C,M,N分别为A1C,BE的中点.如图2.
如图1.在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2CD,DE⊥AB,沿DE将△AEDD折起到△A1ED的位置,连结A1B,A1C,M,N分别为A1C,BE的中点.如图2.
