题目内容
12.已知平面向量$\overrightarrow{a}$、$\overrightarrow{b}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{1}{2}$,若向量$\overrightarrow{c}$满足|$\overrightarrow{a}$-$\overrightarrow{b}$+$\overrightarrow{c}$|≤1,则|$\overrightarrow{c}$|的最大值为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 通过向量的数量积的定义,设出向量的坐标,利用向量的坐标运算和向量的模的公式及几何意义,结合圆的方程即可得出最大值为圆的直径.
解答 解:由平面向量$\overrightarrow{a}$、$\overrightarrow{b}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{1}{2}$,
可得|$\overrightarrow{a}$|•|$\overrightarrow{b}$|•cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=1•1•cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{1}{2}$,
由0≤<$\overrightarrow{a}$,$\overrightarrow{b}$>≤π,可得<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{π}{3}$,
设$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),$\overrightarrow{c}$=(x,y),
则|$\overrightarrow{a}$-$\overrightarrow{b}$+$\overrightarrow{c}$|≤1,即有|($\frac{1}{2}$+x,y-$\frac{\sqrt{3}}{2}$)|≤1,
即为(x+$\frac{1}{2}$)2+(y-$\frac{\sqrt{3}}{2}$)2≤1,
故|$\overrightarrow{a}$-$\overrightarrow{b}$+$\overrightarrow{c}$|≤1的几何意义是在以(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$)为圆心,半径等于1的圆上
和圆内部分,
|$\overrightarrow{c}$|的几何意义是表示向量$\overrightarrow{c}$的终点与原点的距离,而原点在圆上,
则最大值为圆的直径,即为2.
故选:D.
点评 本题主要考查两个向量的数量积的运算,熟练掌握向量的坐标运算和圆的方程及数形结合是解题的关键,属于中档题.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案| A. | [0,1] | B. | (0,1] | C. | [0,1) | D. | (-∞,1] |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
| A. | (-2,0) | B. | (-2,3) | C. | (0,2) | D. | (2,3) |
| A. | 2n | B. | 2n-1 | C. | 2n-1 | D. | 2n-1-1 |
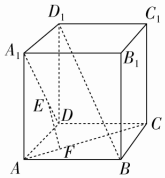 如图所示,在正方体ABCD-A1B1C1D1中,E、F分别在A1D、AC上,且A1E=$\frac{2}{3}$A1D,AF=$\frac{1}{3}$AC,则( )
如图所示,在正方体ABCD-A1B1C1D1中,E、F分别在A1D、AC上,且A1E=$\frac{2}{3}$A1D,AF=$\frac{1}{3}$AC,则( )| A. | EF至多与A1D、AC之一垂直 | B. | EF与A1D、AC都垂直 | ||
| C. | EF与BD1相交 | D. | EF与BD1异面 |
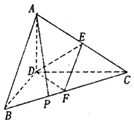 已知三棱锥A-BCD,AD⊥平面BCD,BD⊥CD,AD=BD=2,CD=2$\sqrt{3}$,E,F分别是AC,BC的中点.
已知三棱锥A-BCD,AD⊥平面BCD,BD⊥CD,AD=BD=2,CD=2$\sqrt{3}$,E,F分别是AC,BC的中点.