题目内容
3.已知点M到定点F(1,0)和定直线x=4的距离之比为$\frac{1}{2}$,设动点M的轨迹为曲线C.(1)求曲线C的方程;
(2)设P(4,0),过点F作斜率不为0的直线l与曲线C交于两点A,B,设直线PA,PB的斜率分别是k1,k2,求k1+k2的值.
分析 (1)设点M(x,y),利用条件可得等式$\sqrt{(x-1)^{2}+{y}^{2}}$=$\frac{1}{2}$|x-4|,化简,可得曲线C的轨迹方程;
(2)设直线l的方程为:x=my+1,A(x1,y1),B(x2,y2).联立$\left\{\begin{array}{l}{x=my+1}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$得:(4+3m2)y2+6my-9=0.${k}_{1}+{k}_{2}=\frac{{y}_{1}}{{x}_{1}-4}+\frac{{y}_{2}}{{x}_{2}-4}$=$\frac{{y}_{1}({x}_{2}-4)+{y}_{2}({x}_{1}-4)}{({x}_{1}-4)({x}_{2}-4)}$=$\frac{2m{y}_{1}{y}_{2}-3({y}_{1}+{y}_{2})}{{m}^{2}{y}_{1}{y}_{2}-3m({y}_{1}+{y}_{2})+9}$
解答 解:(1)设点M(x,y),则据题意有$\sqrt{(x-1)^{2}+{y}^{2}}$=$\frac{1}{2}$|x-4|
则4[(x-1)2+y2]=(x-4)2,即3x2+4y2=12,∴$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$
曲线C的方程:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
(2)设直线l的方程为:x=my+1,A(x1,y1),B(x2,y2).
联立$\left\{\begin{array}{l}{x=my+1}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$得:(4+3m2)y2+6my-9=0,${y}_{1}{y}_{2}=\frac{-9}{3{m}^{2}+4},{y}_{1}+{y}_{2}=\frac{-6m}{3+4{m}^{2}}$.
${k}_{1}+{k}_{2}=\frac{{y}_{1}}{{x}_{1}-4}+\frac{{y}_{2}}{{x}_{2}-4}$=$\frac{{y}_{1}({x}_{2}-4)+{y}_{2}({x}_{1}-4)}{({x}_{1}-4)({x}_{2}-4)}$=$\frac{2m{y}_{1}{y}_{2}-3({y}_{1}+{y}_{2})}{{m}^{2}{y}_{1}{y}_{2}-3m({y}_{1}+{y}_{2})+9}$=0.
k1+k2的值为0
点评 本题考查了直线与椭圆的位置关系,属于中档题.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | π |
| A. | $\frac{{y}^{2}}{16}$+$\frac{{x}^{2}}{15}$=1 | B. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{15}$=1 | C. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1 | D. | $\frac{{y}^{2}}{4}$+$\frac{{x}^{2}}{3}$=1 |
| A. | π | B. | 3π | C. | 8π | D. | 9π |
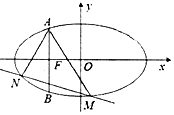 如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左焦点F为抛物线y2=-4x的焦点,过点F做x轴的垂线交椭圆于A,B两点,且|AB|=3.
如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左焦点F为抛物线y2=-4x的焦点,过点F做x轴的垂线交椭圆于A,B两点,且|AB|=3.