题目内容
7.已知α∈R,则“cosα=-$\frac{\sqrt{3}}{2}$”是“α=2kπ+$\frac{5π}{6}$,k∈Z”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
分析 cosα=-$\frac{\sqrt{3}}{2}$,解得α=2kπ±$\frac{5π}{6}$,k∈Z,即可判断出结论.
解答 解:cosα=-$\frac{\sqrt{3}}{2}$,解得α=2kπ±$\frac{5π}{6}$,k∈Z,
∴“cosα=-$\frac{\sqrt{3}}{2}$”是“α=2kπ+$\frac{5π}{6}$,k∈Z”的必要但充分条件.
故选:B.
点评 本题考查了三角函数求值、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
17.已知M是面积为1的△ABC内的一点(不含边界),若△MBC,△MCA和△MAB的面积分别为x,y,z,则$\frac{1}{x+y}$+$\frac{x+y}{z}$的最小值是( )
| A. | 2 | B. | 3 | C. | 3.5 | D. | 4 |
15.设一圆锥的外接球与内切球的球心位置相同,且外接球的半径为2,则该圆锥的体积为( )
| A. | π | B. | 3π | C. | 8π | D. | 9π |
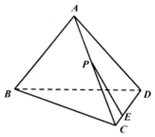 如图,已知三棱锥A-BCD的所有棱长均相等,点E满足$\overrightarrow{DE}$=3$\overrightarrow{EC}$,点P在棱AC上运动,设EP与平面BCD所成角为θ,则sinθ的最大值为$\frac{2\sqrt{2}}{3}$.
如图,已知三棱锥A-BCD的所有棱长均相等,点E满足$\overrightarrow{DE}$=3$\overrightarrow{EC}$,点P在棱AC上运动,设EP与平面BCD所成角为θ,则sinθ的最大值为$\frac{2\sqrt{2}}{3}$.