题目内容
4.设集合A={x|x2-3x<0},B={x|x2>4},则A∩B=( )| A. | (-2,0) | B. | (-2,3) | C. | (0,2) | D. | (2,3) |
分析 分别求出关于A、B的不等式,求出A、B的交集即可.
解答 解:A={x|x2-3x<0}={x|0<x<3},
B={x|x2>4}={x|x>2或x<-2},
则A∩B={x|2<x<3},
故选:D.
点评 本题考查了集合的交集的运算,考查不等式问题,是一道基础题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
15.设一圆锥的外接球与内切球的球心位置相同,且外接球的半径为2,则该圆锥的体积为( )
| A. | π | B. | 3π | C. | 8π | D. | 9π |
9.如图所示是一个几何体的三视图,则这个几何体外接球的体积为( )
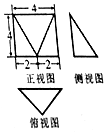

| A. | 36π | B. | $\frac{64\sqrt{2}}{3}$π | C. | 8$\sqrt{6}$π | D. | $\frac{8}{3}$π |
2.当0<a<1时,函数y=loga(x2-4x+3)的单调增区间为( )
| A. | (-∞,2] | B. | [2,+∞) | C. | (-∞,1) | D. | (3,+∞) |
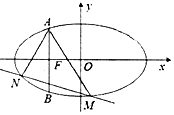 如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左焦点F为抛物线y2=-4x的焦点,过点F做x轴的垂线交椭圆于A,B两点,且|AB|=3.
如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左焦点F为抛物线y2=-4x的焦点,过点F做x轴的垂线交椭圆于A,B两点,且|AB|=3.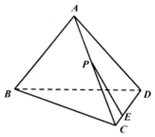 如图,已知三棱锥A-BCD的所有棱长均相等,点E满足$\overrightarrow{DE}$=3$\overrightarrow{EC}$,点P在棱AC上运动,设EP与平面BCD所成角为θ,则sinθ的最大值为$\frac{2\sqrt{2}}{3}$.
如图,已知三棱锥A-BCD的所有棱长均相等,点E满足$\overrightarrow{DE}$=3$\overrightarrow{EC}$,点P在棱AC上运动,设EP与平面BCD所成角为θ,则sinθ的最大值为$\frac{2\sqrt{2}}{3}$.