题目内容
在平面直角坐标系xOy中,已知椭圆C1:  +
+ =1(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.
=1(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.
(1)求椭圆C1的方程;
(2)设直线l同时与椭圆C1和抛物线C2:y2=4x相切,求直线l的方程.
解:(1)因为椭圆C1的左焦点为F1(-1,0),
所以c=1.
将点P(0,1)代入椭圆方程 +
+ =1,
=1,
得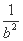 =1,即b=1.
=1,即b=1.
所以a2=b2+c2=2.
所以椭圆C1的方程为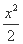 +y2=1.
+y2=1.
(2)由题意可知,直线l的斜率显然存在且不等于0,
设直线l的方程为y=kx+m,
由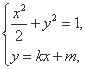
消去y并整理得(1+2k2)x2+4kmx+2m2-2=0.
因为直线l与椭圆C1相切,
所以Δ1=16k2m2-4(1+2k2)(2m2-2)=0.
整理得2k2-m2+1=0.①
由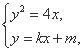 消去y并整理得k2x2+(2km-4)x+m2=0.
消去y并整理得k2x2+(2km-4)x+m2=0.
因为直线l与抛物线C2相切,
所以Δ2=(2km-4)2-4k2m2=0,
整理得km=1.②
综合①②,解得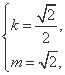 或
或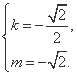
所以直线l的方程为y=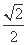 x+
x+ 或y=-
或y=-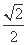 x-
x- .
.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
某学生对其亲属30人的饮食习惯进行了一次调查,并用茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
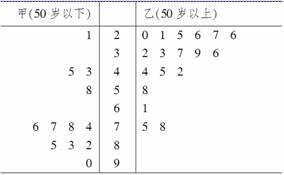
(1)根据茎叶图,帮助这位学生说明其亲属30人的饮食习惯;
(2)根据以上数据完成下列2×2的列联表:
|
| 主食蔬菜 | 主食肉类 | 合计 |
| 50岁以下 | |||
| 50岁以上 | |||
| 合计 |
(3)能否有99%的把握认为其亲属的饮食习惯与年龄有关,并写出简要分析.
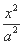 -
-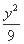 =1(a>0)的渐近线方程为3x±2y=0,则a的值为( )
=1(a>0)的渐近线方程为3x±2y=0,则a的值为( ) +
+ =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,a+b=3.
,a+b=3.
 (B)
(B)
 (D)
(D)
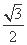 .双曲线x2-y2=1的渐近线与椭圆C有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为( )
.双曲线x2-y2=1的渐近线与椭圆C有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为( )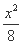 +
+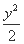 =1 (B)
=1 (B) 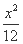 +
+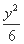 =1
=1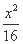 +
+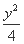 =1 (D)
=1 (D)  +
+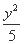 =1
=1 ,则C的实轴长为( )
,则C的实轴长为( ) ,则抛物线的方程为( )
,则抛物线的方程为( )