题目内容
已知抛物线的顶点在原点,焦点在x轴的正半轴上,若抛物线的准线与双曲线5x2-y2=20的两条渐近线围成的三角形的面积等于4 ,则抛物线的方程为( )
,则抛物线的方程为( )
(A)y2=4x (B)x2=4y
(C)y2=8x (D)x2=8y
C
解析:设抛物线方程为y2=2px(p>0),
则准线方程为x=-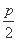 ,
,
双曲线5x2-y2=20的渐近线方程为y=± x,
x,
抛物线的准线与双曲线渐近线的交点分别为P1(-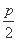 ,
,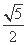 p),P2(-
p),P2(-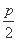 ,-
,-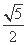 p).
p).
∴ =
= |P1P2|·
|P1P2|·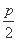
= ·
· p·
p·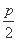
=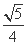 p2=4
p2=4 .
.
∴p2=16,p=4,
∴抛物线方程为y2=8x.故选C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某工厂对200个电子元件的使用寿命进行检查,按照使用寿命(单位:h),可以把这批电子元件分成第一组[100,200],第二组(200,300],第三组(300,400],第四组(400,500],第五组(500,600],第六组(600,700],由于工作中不慎将部分数据丢失,现有以下部分图表:

| 分组 | [100,200] | (200,300] | (300,400] | (400,500] | (500,600] | (600,700] |
| 频数 | B | 30 | E | F | 20 | H |
| 频率 | C | D | 0.2 | 0.4 | G | I |
(1)求图2中的A及表格中的B,C,D,E,F,G,H,I的值;
(2)求图2中阴影部分的面积;
(3)若电子元件的使用时间超过300h为合格产品,求这批电子元件合格的概率.
 ,则C的方程是( )
,则C的方程是( ) +
+  =1 (B)
=1 (B)  +
+ =1
=1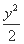 =1 (D)
=1 (D)  =1
=1 +
+ =1(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.
=1(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.
 (B)
(B) (C)
(C)
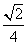 B.
B.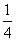
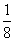 D.
D.