题目内容
已知等差数列{an}的公差不为零,a1=25且a1、a11、a13成等比数列.
(Ⅰ)求{an}的通项公式;
(Ⅱ)若a1+a3+a5+…+a2n-1=70,求n的值.
(Ⅰ)求{an}的通项公式;
(Ⅱ)若a1+a3+a5+…+a2n-1=70,求n的值.
考点:数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件利用等差数列的通项公式和等比数列的性质求出公差,由此能求出an=-2n+27.
(Ⅱ)由an=-2n+27,得{a2n-1}是首项为a1=25,公差为d=-4的等差数列,所以a1+a3+…+a2n-1=27n-2n2,由此根据a1+a3+a5+…+a2n-1=70,得27n-2n2=70,从而能求出n的值.
(Ⅱ)由an=-2n+27,得{a2n-1}是首项为a1=25,公差为d=-4的等差数列,所以a1+a3+…+a2n-1=27n-2n2,由此根据a1+a3+a5+…+a2n-1=70,得27n-2n2=70,从而能求出n的值.
解答:
解:(Ⅰ)设{an}的公差为d,由题意得a112=a1a13,
∴(a1+10d)2=a1(a1+12d),
∵a1=25,∴d=0(舍),或d=-2,
∴an=25+(n-1)×(-2)=-2n+27.
(Ⅱ)∵an=-2n+27,
∴a2n-1=-2(2n-1)+27=-4n+29,
∴{a2n-1}是首项为a1=25,公差为d=-4的等差数列,
∴a1+a3+…+a2n-1
=
(a1+a2n-1)
=27n-2n2,
∵a1+a3+a5+…+a2n-1=70,
∴27n-2n2=70,
解得n=10或n=
(舍),
∴n=10.
∴(a1+10d)2=a1(a1+12d),
∵a1=25,∴d=0(舍),或d=-2,
∴an=25+(n-1)×(-2)=-2n+27.
(Ⅱ)∵an=-2n+27,
∴a2n-1=-2(2n-1)+27=-4n+29,
∴{a2n-1}是首项为a1=25,公差为d=-4的等差数列,
∴a1+a3+…+a2n-1
=
| n |
| 2 |
=27n-2n2,
∵a1+a3+a5+…+a2n-1=70,
∴27n-2n2=70,
解得n=10或n=
| 7 |
| 2 |
∴n=10.
点评:本题考查数列的通项公式的求法,考查数列的项数n的求法,解题时要认真审题,注意等差数列的性质的灵活运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
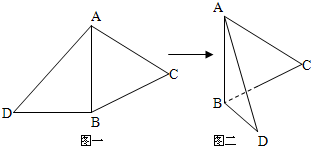 如图一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2.将△ABD沿边AB折起,使得△ABD与△ABC成直二面角D-AB-C,如图二,在二面角D-AB-C中.
如图一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2.将△ABD沿边AB折起,使得△ABD与△ABC成直二面角D-AB-C,如图二,在二面角D-AB-C中.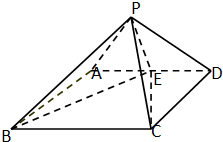 如图,四棱锥P-ABCD的底面是矩形,侧面PAD⊥底面ABCD,在△PAD中
如图,四棱锥P-ABCD的底面是矩形,侧面PAD⊥底面ABCD,在△PAD中 如图,在底面边长为a的正方形的四棱锥P-ABCD中,已知PA⊥平面AC,且PA=a,则直线PB与平面PCD所成的角大小为
如图,在底面边长为a的正方形的四棱锥P-ABCD中,已知PA⊥平面AC,且PA=a,则直线PB与平面PCD所成的角大小为