题目内容

设函数f（x）=x（ex-1）-
1
2
x2，求函数f（x）的单调增区间．
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：由f′（x）=（ex-1）（x+1），令f′（x）＞0，解得：x＞0，x＜-1，从而求出函数f（x）在（-∞，-1）和（0，+∞）递增．
解答： 解：∵f′（x）=（ex-1）（x+1），
令f′（x）＞0，解得：x＞0，x＜-1，
∴f（x）在（-∞，-1）和（0，+∞）递增．
点评：本题考察了函数的单调性，导数的应用，是的基础题．
练习册系列答案
相关题目
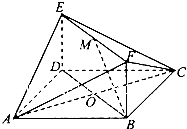如图，已知正方形ABCD和矩形BDFE所在的平面互相垂直，AC交BD于O点，M为EF的中点，BC=
2
，BF=1
（Ⅰ）求证：BC⊥AF：
（Ⅱ）求证：BM∥平面ACE；
（Ⅲ）求二面角B-AF-C的大小．
已知等差数列{an}的公差不为零，a1=25且a1、a11、a13成等比数列．
（Ⅰ）求{an}的通项公式；
（Ⅱ）若a1+a3+a5+…+a2n-1=70，求n的值．
设函数f（x）=ex-ax-2，其导函数为f′（x）．
（1）若a=1，求函数f（x）在点（0，f（0））处的切线方程；
（2）求f（x）的单调区间；
（3）若k为整数，若x＞0时，k＜
x+1
ex-1
+x恒成立，试求k的最大值．
已知数列{an}的各项均为正整数，且a1=1，a2=4，an=
an-1an+1+1
，n≥2，n∈N*．
（1）求a3，a4的值；
（2）求证：对一切正整数n，2anan+1+1是完全平方数．
已知关于x的不等式：|2x-m|≤1的整数解有且仅有一个值为2．
（Ⅰ）求整数m的值；
（Ⅱ）已知a，b，c∈R，若4a4+4b4+4c4=m，求a2+b2+c2的最大值．
已知f′（x）是f（x）的导函数，f（x）=ln（x+1）+m-2f′（1），m∈R，且函数f（x）的图象过点（0，-2）．
（1）求函数y=f（x）的表达式；
（2）求函数g（x）=f（x）+x+
6
x+1
的单调区间和极值．
已知Sn是数列{an}的前n项和，若Sn=2n-1，则a1=
 
．
在等差数列{an}中，已知a3=5，a1+a2+…+a7=49
（Ⅰ）求an；
（Ⅱ）若bn=
1
anan+1
（n∈N*），求数列{bn}的前n项和Sn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网