题目内容
4.(Ⅰ)解不等式-x2+4x+5<0;(Ⅱ)解不等式$\frac{2x-1}{3x+1}$>1.
分析 (Ⅰ)先因式分解即可求出答案,
(Ⅱ)把原不等式化为(x+2)(3x+1)<0,解的即可
解答 解:(Ⅰ)-x2+4x+5<0,
即为x2-4x-5>0,
即(x+1)(x-5)>0,
解得x<-1或x>5,
故原不等式的解集为(-∞,-1)∪(5,+∞),
(Ⅱ)由$\frac{2x-1}{3x+1}$>1,
即为$\frac{2x-1}{3x+1}$-1>0,
即为$\frac{-x-2}{3x+1}$>0,
即(x+2)(3x+1)<0,
解得-2<x<-$\frac{1}{3}$.
故原不等式的解集为(-2,-$\frac{1}{3}$)
点评 本题考查了一元二次不等式和分式不等式的解法,属于基础题

练习册系列答案
相关题目
19.已知曲线C:$y=\frac{1}{3}{x^3}-{x^2}-4x+1$,直线l:x+y+2k-1=0,当x∈[-3,3]时,直线l恒在曲线C的上方,则实数k的取值范围是( )
| A. | $k>-\frac{5}{6}$ | B. | $k<-\frac{5}{6}$ | C. | $k<-\frac{3}{4}$ | D. | $k>-\frac{3}{4}$ |
9.甲、乙两艘货轮都要在某个泊位停靠6小时,假定它们在一昼夜的时间段中随即到达,则两船中有一艘在停泊位时,另一艘船必须等待的概率为( )
| A. | $\frac{7}{16}$ | B. | $\frac{9}{16}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{6}$ |
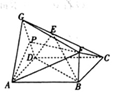 如图所示的多面体中,底面ABCD为正方形,△GAD为等边三角形,∠GDC=90°,点E是线段GC上除两端点外的一点.
如图所示的多面体中,底面ABCD为正方形,△GAD为等边三角形,∠GDC=90°,点E是线段GC上除两端点外的一点. 满足
满足 ,则
,则 的最大值为
的最大值为 B.
B. C.1 D.
C.1 D.