题目内容
9.甲、乙两艘货轮都要在某个泊位停靠6小时,假定它们在一昼夜的时间段中随即到达,则两船中有一艘在停泊位时,另一艘船必须等待的概率为( )| A. | $\frac{7}{16}$ | B. | $\frac{9}{16}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{6}$ |
分析 先确定概率类型是几何概型中的面积类型,再设甲到x点,乙到y点,建立甲先到,乙先到满足的条件,再画出并求解0<x<24,0<y<24可行域面积,再求出满足条件的可行域面积,由概率公式求解.
解答 解:设甲、乙两船到达泊位的时刻分别为x,y.则作出如图所示的区域.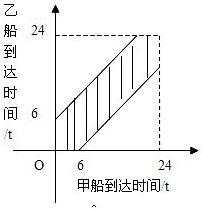
本题中,区域D的面积S1=242,
区域d的面积S2=242-182.
∴P=$\frac{{S}_{2}}{{S}_{1}}$=$\frac{2{4}^{2}-1{8}^{2}}{2{4}^{2}}$=$\frac{7}{16}$
即两船中有一艘在停泊位时另一船必须等待的概率为$\frac{7}{16}$.
故选:A
点评 本题主要考查建模、解模能力;解答关键是利用线性规划作出事件对应的平面区域,再利用几何概型概率公式求出事件的概率.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
1.已知函数$f(x)=4{sin^2}x+4\sqrt{3}sinxcosx+5$,若不等式f(x)≤m在$[0,\frac{π}{2}]$上有解,则实数m的最小值为( )
| A. | 5 | B. | -5 | C. | 11 | D. | -11 |
17.已知$\frac{{{a^2}+2a+2}}{x}≤$$\frac{4}{{{x^2}-x}}+1$对于任意的x∈(1,+∞)恒成立,则( )
| A. | a的最小值为-3 | B. | a的最小值为-4 | C. | a的最大值为2 | D. | a的最大值为4 |
14.设$0<α<β<\frac{π}{2},sinα=\frac{3}{5},cos(β-α)=\frac{12}{13}$,则sinβ的值为( )
| A. | $\frac{16}{65}$ | B. | $\frac{33}{65}$ | C. | $\frac{56}{65}$ | D. | $\frac{63}{65}$ |
18.已知点A(0,-1)是抛物线C:x2=2py(p>0)准线上的一点,点F是抛物线C的焦点,点P在抛物线C上且满足|PF|=m|PA|,当m取最小值时,点P恰好在以原点为中心,F为焦点的双曲线上,则此双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$+1 | D. | $\sqrt{3}$+1 |
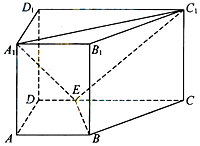 如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD=$\sqrt{2}$,AA1=3,E为CD上一点,DE=1,EC=3
如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD=$\sqrt{2}$,AA1=3,E为CD上一点,DE=1,EC=3