Question

已知函数f（x）=x²-2|x|-3．
（1）作出函数f（x）的图象，并根据图象写出函数f（x）的单调区间，以及在各单调区间的奇偶性；
（2）求函数f（x）在x∈（-2，4]时的最大值与最小值．

Answer 1

考点：分段函数的应用,函数的图象

专题：作图题,数形结合,函数的性质及应用

分析：（1）作出函数f（x）的图象，当x≥0时f（x）x²-2x-3，增区间为（1，+∞），减区间为（0，1]，当x＜0时f（x）=x²+2x-3，增区间为（-1，0]，减区间为（-∞，-1]；
（2）结合图象可知最小值，f（1）=f（-1）=-4，最大值f（4）=5．

解答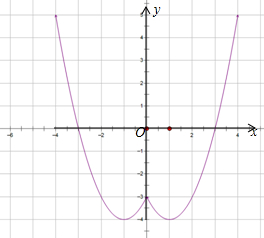： 解：（1）函数f（x）=x²-2|x|-3=

x2-2x-3，x≥0 x2+2x-3，x＜0

，
图象如右图所示：
由图可得：
函数f（x）的单调区间有：（-∞，-1]，（-1，0]，（0，1]，（1，+∞），
函数f（x）的在区间（-∞，-1]，（0，1]上单调递减，
函数f（x）的在区间（-1，0]，（1，+∞]上单调递增．
（2）由图可得：
当x∈（-2，4]时，
当x=±1时，函数f（x）的最小值为-4，
当x=4时，函数f（x）的最大值为5．

点评：本题考查带绝对值的函数的图象，考查函数的单调区间和最值情况，考查数形结合的思想方法，属于基础题．